PBWR: Parametric Building Wireframe Reconstruction from Aerial LiDAR Point Clouds

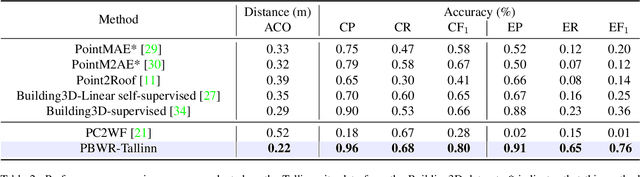
In this paper, we present an end-to-end 3D building wireframe reconstruction method to regress edges directly from aerial LiDAR point clouds.Our method, named Parametric Building Wireframe Reconstruction (PBWR), takes aerial LiDAR point clouds and initial edge entities as input, and fully uses self-attention mechanism of transformers to regress edge parameters without any intermediate steps such as corner prediction. We propose an edge non-maximum suppression (E-NMS) module based on edge similarityto remove redundant edges. Additionally, a dedicated edge loss function is utilized to guide the PBWR in regressing edges parameters, where simple use of edge distance loss isn't suitable. In our experiments, we demonstrate state-of-the-art results on the Building3D dataset, achieving an improvement of approximately 36% in entry-level dataset edge accuracy and around 42% improvement in the Tallinn dataset.

Graph Convolutional Networks for Simulating Multi-phase Flow and Transport in Porous Media

Numerical simulation of multi-phase fluid dynamics in porous media is critical for many subsurface applications. Data-driven surrogate modeling provides computationally inexpensive alternatives to high-fidelity numerical simulators. While the commonly used convolutional neural networks (CNNs) are powerful in approximating partial differential equation solutions, it remains challenging for CNNs to handle irregular and unstructured simulation meshes. However, subsurface simulation models often involve unstructured meshes with complex mesh geometries, which limits the application of CNNs. To address this challenge, here we construct surrogate models based on Graph Convolutional Networks (GCNs) to approximate the spatial-temporal solutions of multi-phase flow and transport processes. We propose a new GCN architecture suited to the hyperbolic character of the coupled PDE system, to better capture the saturation dynamics. Results of 2D heterogeneous test cases show that our surrogates predict the evolutions of the pressure and saturation states with high accuracy, and the predicted rollouts remain stable for multiple timesteps. Moreover, the GCN-based models generalize well to irregular domain geometries and unstructured meshes that are unseen in the training dataset.