Bishshoy Das
On Characterizing the Evolution of Embedding Space of Neural Networks using Algebraic Topology
Nov 09, 2023Abstract:We study how the topology of feature embedding space changes as it passes through the layers of a well-trained deep neural network (DNN) through Betti numbers. Motivated by existing studies using simplicial complexes on shallow fully connected networks (FCN), we present an extended analysis using Cubical homology instead, with a variety of popular deep architectures and real image datasets. We demonstrate that as depth increases, a topologically complicated dataset is transformed into a simple one, resulting in Betti numbers attaining their lowest possible value. The rate of decay in topological complexity (as a metric) helps quantify the impact of architectural choices on the generalization ability. Interestingly from a representation learning perspective, we highlight several invariances such as topological invariance of (1) an architecture on similar datasets; (2) embedding space of a dataset for architectures of variable depth; (3) embedding space to input resolution/size, and (4) data sub-sampling. In order to further demonstrate the link between expressivity \& the generalization capability of a network, we consider the task of ranking pre-trained models for downstream classification task (transfer learning). Compared to existing approaches, the proposed metric has a better correlation to the actually achievable accuracy via fine-tuning the pre-trained model.
Softmax Gradient Tampering: Decoupling the Backward Pass for Improved Fitting
Nov 24, 2021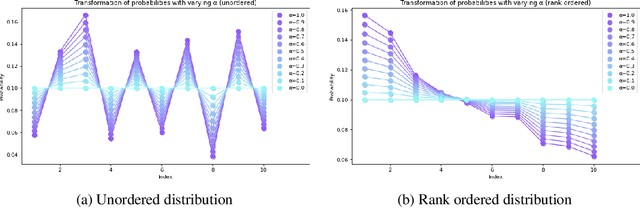
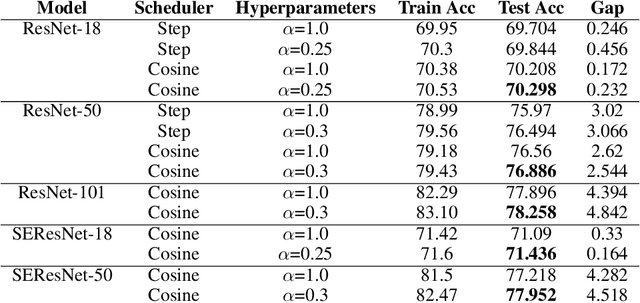
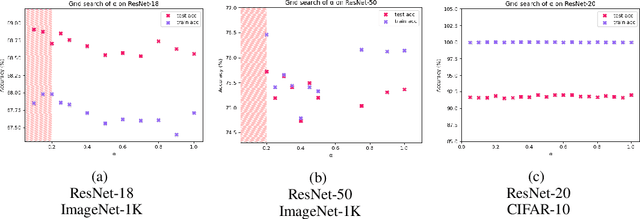

Abstract:We introduce Softmax Gradient Tampering, a technique for modifying the gradients in the backward pass of neural networks in order to enhance their accuracy. Our approach transforms the predicted probability values using a power-based probability transformation and then recomputes the gradients in the backward pass. This modification results in a smoother gradient profile, which we demonstrate empirically and theoretically. We do a grid search for the transform parameters on residual networks. We demonstrate that modifying the softmax gradients in ConvNets may result in increased training accuracy, thus increasing the fit across the training data and maximally utilizing the learning capacity of neural networks. We get better test metrics and lower generalization gaps when combined with regularization techniques such as label smoothing. Softmax gradient tampering improves ResNet-50's test accuracy by $0.52\%$ over the baseline on the ImageNet dataset. Our approach is very generic and may be used across a wide range of different network architectures and datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge