Join, select, and insert: efficient out-of-core algorithms for hierarchical segmentation trees

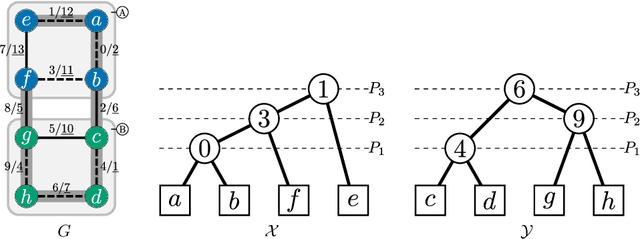
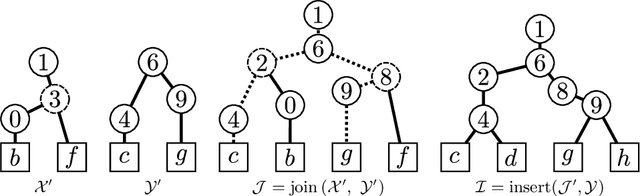
Binary Partition Hierarchies (BPH) and minimum spanning trees are fundamental data structures involved in hierarchical analysis such as quasi-flat zones or watershed. However, classical BPH construction algorithms require to have the whole data in memory, which prevent the processing of large images that cannot fit entirely in the main memory of the computer. To cope with this problem, an algebraic framework leading to a high level calculus was introduced allowing an out-of-core computation of BPHs. This calculus relies on three operations: select, join, and insert. In this article, we introduce three efficient algorithms to perform these operations providing pseudo-code and complexity analysis.

Efficient Multiscale Object-based Superpixel Framework

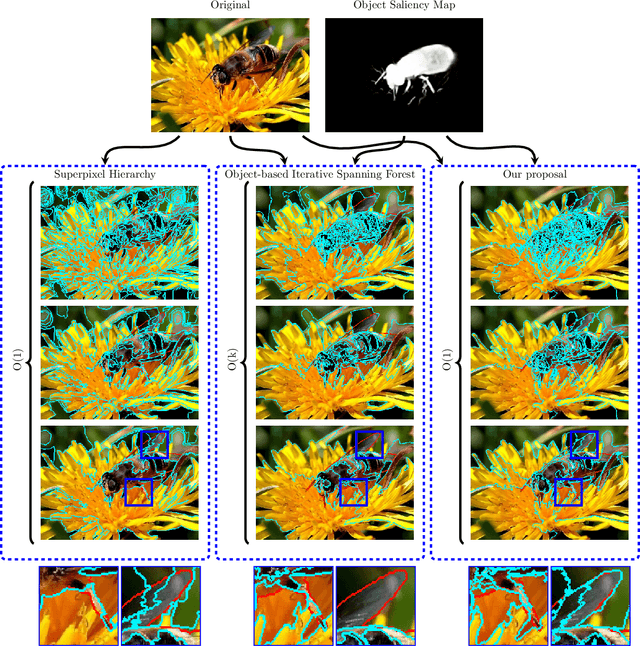
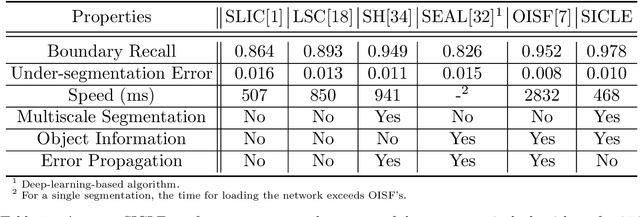
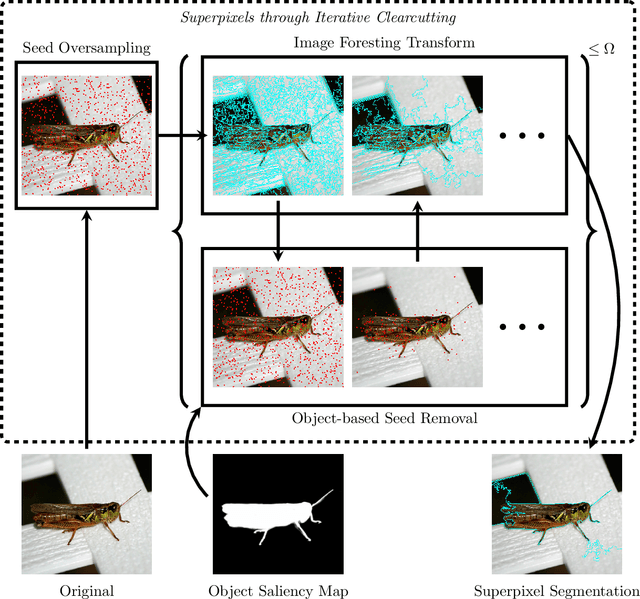
Superpixel segmentation can be used as an intermediary step in many applications, often to improve object delineation and reduce computer workload. However, classical methods do not incorporate information about the desired object. Deep-learning-based approaches consider object information, but their delineation performance depends on data annotation. Additionally, the computational time of object-based methods is usually much higher than desired. In this work, we propose a novel superpixel framework, named Superpixels through Iterative CLEarcutting (SICLE), which exploits object information being able to generate a multiscale segmentation on-the-fly. SICLE starts off from seed oversampling and repeats optimal connectivity-based superpixel delineation and object-based seed removal until a desired number of superpixels is reached. It generalizes recent superpixel methods, surpassing them and other state-of-the-art approaches in efficiency and effectiveness according to multiple delineation metrics.

Component Tree Loss Function: Definition and Optimization

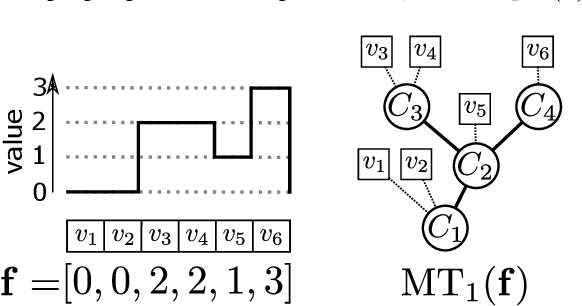
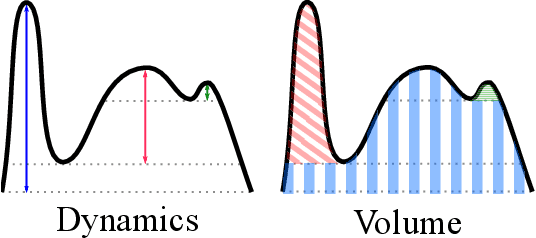
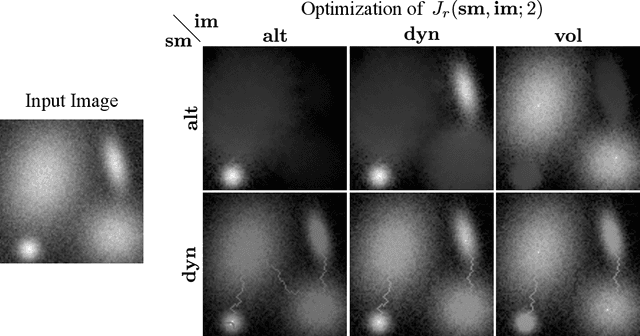
In this article, we propose a method to design loss functions based on component trees which can be optimized by gradient descent algorithms and which are therefore usable in conjunction with recent machine learning approaches such as neural networks. We show how the altitudes associated to the nodes of such hierarchical image representations can be differentiated with respect to the image pixel values. This feature is used to design a generic loss function that can select or discard image maxima based on various attributes such as extinction values. The possibilities of the proposed method are demonstrated on simulated and real image filtering.

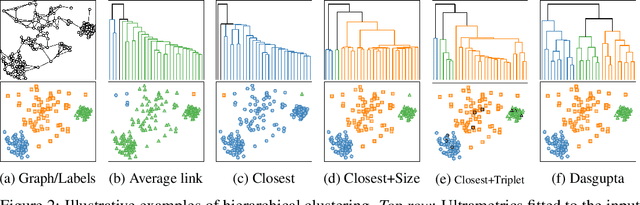
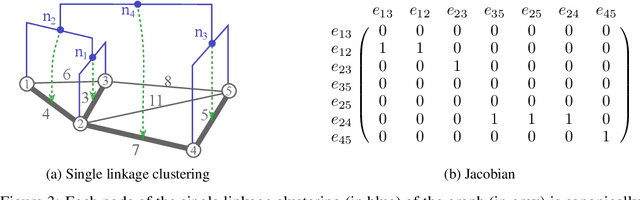
Ultrametric Fitting by Gradient Descent

We study the problem of fitting an ultrametric distance to a dissimilarity graph in the context of hierarchical cluster analysis. Standard hierarchical clustering methods are specified procedurally, rather than in terms of the cost function to be optimized. We aim to overcome this limitation by presenting a general optimization framework for ultrametric fitting. Our approach consists of modeling the latter as a constrained optimization problem over the continuous space of ultrametrics. So doing, we can leverage the simple, yet effective, idea of replacing the ultrametric constraint with an equivalent min-max operation injected directly into the cost function. The proposed reformulation leads to an unconstrained optimization problem that can be efficiently solved by gradient descent methods. The flexibility of our framework allows us to investigate several cost functions, following the classic paradigm of combining a data fidelity term with a regularization. While we provide no theoretical guarantee to find the global optimum, the numerical results obtained over a number of synthetic and real datasets demonstrate the good performance of our approach with respect to state-of-the-art agglomerative algorithms. This makes us believe that the proposed framework sheds new light on the way to design a new generation of hierarchical clustering methods.