Join, select, and insert: efficient out-of-core algorithms for hierarchical segmentation trees
Paper and Code
Oct 05, 2022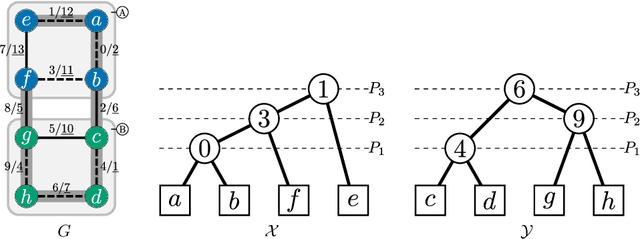
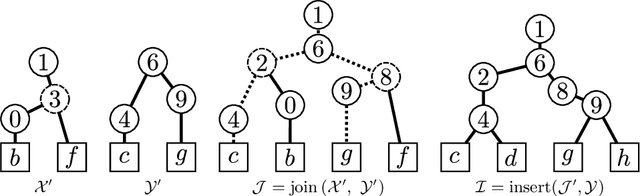
Binary Partition Hierarchies (BPH) and minimum spanning trees are fundamental data structures involved in hierarchical analysis such as quasi-flat zones or watershed. However, classical BPH construction algorithms require to have the whole data in memory, which prevent the processing of large images that cannot fit entirely in the main memory of the computer. To cope with this problem, an algebraic framework leading to a high level calculus was introduced allowing an out-of-core computation of BPHs. This calculus relies on three operations: select, join, and insert. In this article, we introduce three efficient algorithms to perform these operations providing pseudo-code and complexity analysis.
* IAPR International Conference on Discrete Geometry and
Mathematical Morphology (DGMM), Oct 2022, Strasbourg, France
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge