Structure-Preserving Transformers for Learning Parametrized Hamiltonian Systems

Two of the many trends in neural network research of the past few years have been (i) the learning of dynamical systems, especially with recurrent neural networks such as long short-term memory networks (LSTMs) and (ii) the introduction of transformer neural networks for natural language processing (NLP) tasks. Both of these trends have created enormous amounts of traction, particularly the second one: transformer networks now dominate the field of NLP. Even though some work has been performed on the intersection of these two trends, this work was largely limited to using the vanilla transformer directly without adjusting its architecture for the setting of a physical system. In this work we use a transformer-inspired neural network to learn a complicated non-linear dynamical system and furthermore (for the first time) imbue it with structure-preserving properties to improve long-term stability. This is shown to be extremely important when applying the neural network to real world applications.

Symplectic Autoencoders for Model Reduction of Hamiltonian Systems

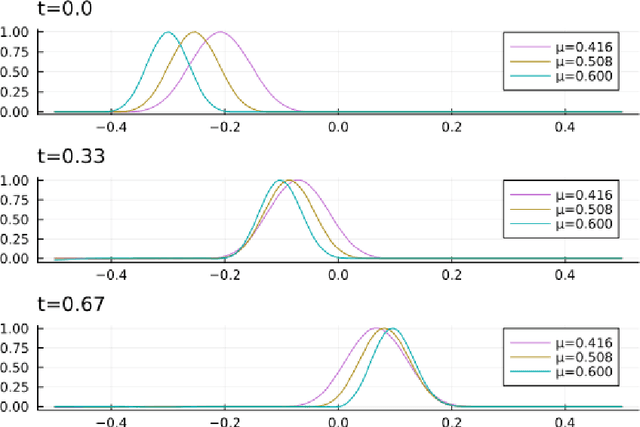
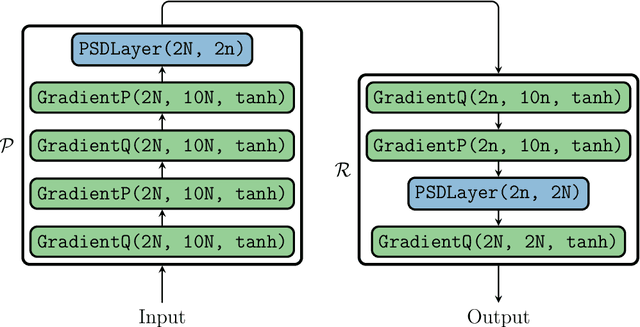
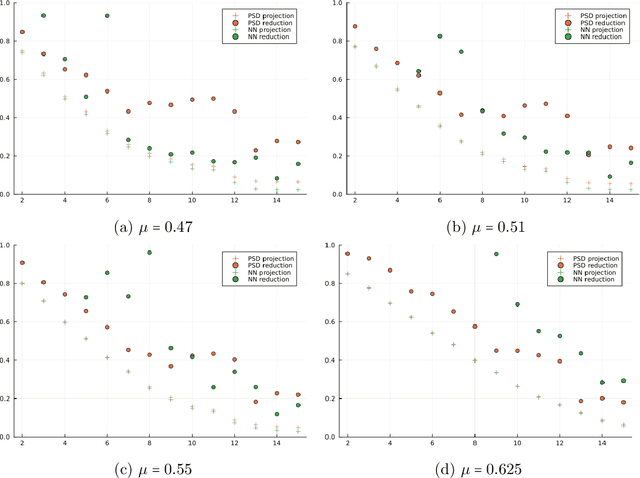
Many applications, such as optimization, uncertainty quantification and inverse problems, require repeatedly performing simulations of large-dimensional physical systems for different choices of parameters. This can be prohibitively expensive. In order to save computational cost, one can construct surrogate models by expressing the system in a low-dimensional basis, obtained from training data. This is referred to as model reduction. Past investigations have shown that, when performing model reduction of Hamiltonian systems, it is crucial to preserve the symplectic structure associated with the system in order to ensure long-term numerical stability. Up to this point structure-preserving reductions have largely been limited to linear transformations. We propose a new neural network architecture in the spirit of autoencoders, which are established tools for dimension reduction and feature extraction in data science, to obtain more general mappings. In order to train the network, a non-standard gradient descent approach is applied that leverages the differential-geometric structure emerging from the network design. The new architecture is shown to significantly outperform existing designs in accuracy.

Generalizing Adam To Manifolds For Efficiently Training Transformers

One of the primary reasons behind the success of neural networks has been the emergence of an array of new, highly-successful optimizers, perhaps most importantly the Adam optimizer. It is wiedely used for training neural networks, yet notoriously hard to interpret. Lacking a clear physical intuition, Adam is difficult to generalize to manifolds. Some attempts have been made to directly apply parts of the Adam algorithm to manifolds or to find an underlying structure, but a full generalization has remained elusive. In this work a new approach is presented that leverages the special structure of the manifolds which are relevant for optimization of neural networks, such as the Stiefel manifold, the symplectic Stiefel manifold, the Grassmann manifold and the symplectic Grassmann manifold: all of these are homogeneous spaces and as such admit a global tangent space representation. This global tangent space representation is used to perform all of the steps in the Adam optimizer. The resulting algorithm is then applied to train a transformer for which orthogonality constraints are enforced up to machine precision and we observe significant speed-ups in the training process. Optimization of neural networks where they weights do not lie on a manifold is identified as a special case of the presented framkework. This allows for a flexible implementation in which the learning rate is adapted simultaneously for all parameters, irrespective of whether they are an element of a general manifold or a vector space.