Symplectic Autoencoders for Model Reduction of Hamiltonian Systems
Paper and Code
Dec 15, 2023
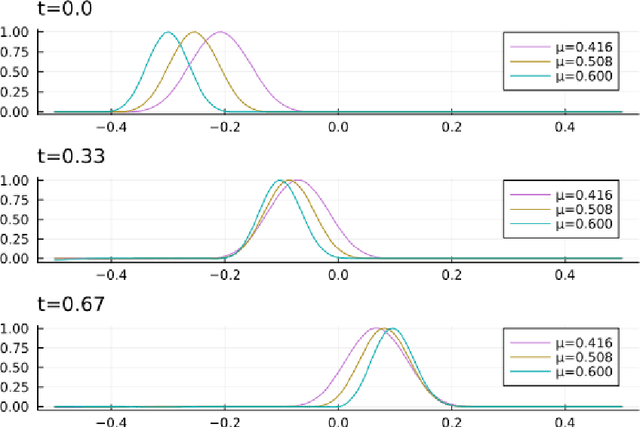
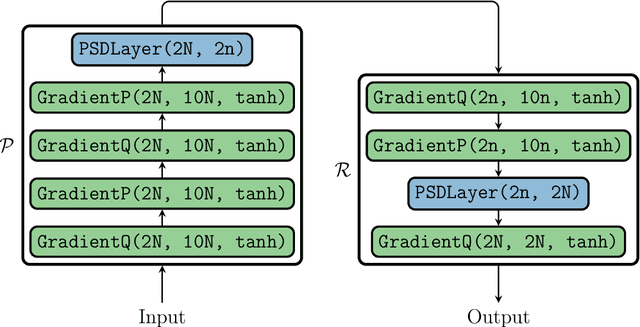
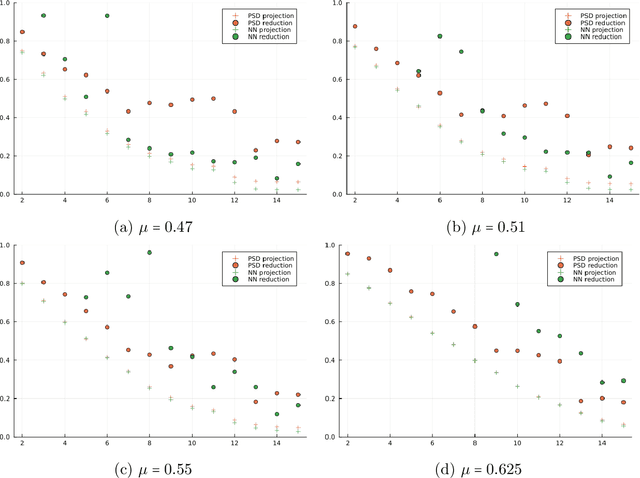
Many applications, such as optimization, uncertainty quantification and inverse problems, require repeatedly performing simulations of large-dimensional physical systems for different choices of parameters. This can be prohibitively expensive. In order to save computational cost, one can construct surrogate models by expressing the system in a low-dimensional basis, obtained from training data. This is referred to as model reduction. Past investigations have shown that, when performing model reduction of Hamiltonian systems, it is crucial to preserve the symplectic structure associated with the system in order to ensure long-term numerical stability. Up to this point structure-preserving reductions have largely been limited to linear transformations. We propose a new neural network architecture in the spirit of autoencoders, which are established tools for dimension reduction and feature extraction in data science, to obtain more general mappings. In order to train the network, a non-standard gradient descent approach is applied that leverages the differential-geometric structure emerging from the network design. The new architecture is shown to significantly outperform existing designs in accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge