Beyond Supervised Continual Learning: a Review

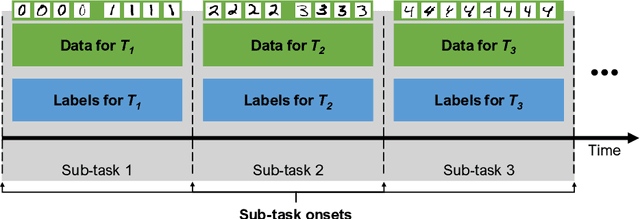
Continual Learning (CL, sometimes also termed incremental learning) is a flavor of machine learning where the usual assumption of stationary data distribution is relaxed or omitted. When naively applying, e.g., DNNs in CL problems, changes in the data distribution can cause the so-called catastrophic forgetting (CF) effect: an abrupt loss of previous knowledge. Although many significant contributions to enabling CL have been made in recent years, most works address supervised (classification) problems. This article reviews literature that study CL in other settings, such as learning with reduced supervision, fully unsupervised learning, and reinforcement learning. Besides proposing a simple schema for classifying CL approaches w.r.t. their level of autonomy and supervision, we discuss the specific challenges associated with each setting and the potential contributions to the field of CL in general.

A Study of Continual Learning Methods for Q-Learning

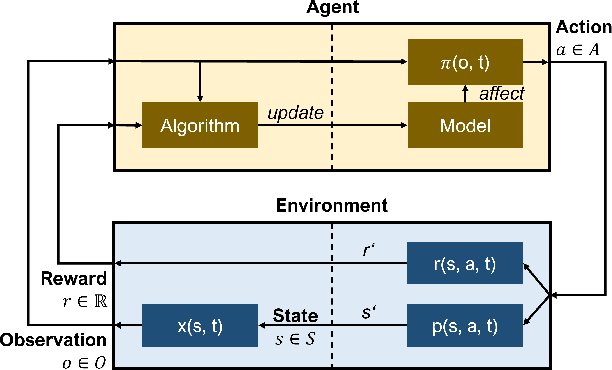
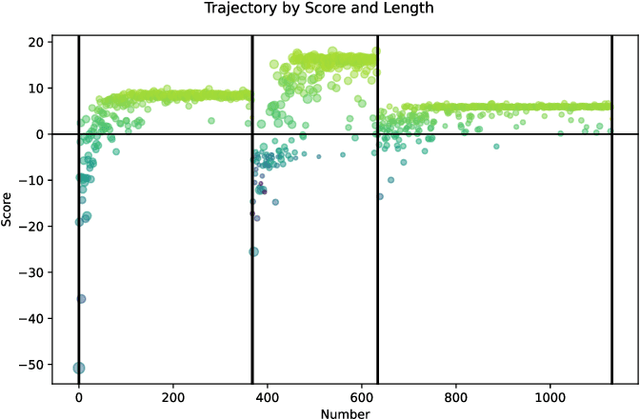
We present an empirical study on the use of continual learning (CL) methods in a reinforcement learning (RL) scenario, which, to the best of our knowledge, has not been described before. CL is a very active recent research topic concerned with machine learning under non-stationary data distributions. Although this naturally applies to RL, the use of dedicated CL methods is still uncommon. This may be due to the fact that CL methods often assume a decomposition of CL problems into disjoint sub-tasks of stationary distribution, that the onset of these sub-tasks is known, and that sub-tasks are non-contradictory. In this study, we perform an empirical comparison of selected CL methods in a RL problem where a physically simulated robot must follow a racetrack by vision. In order to make CL methods applicable, we restrict the RL setting and introduce non-conflicting subtasks of known onset, which are however not disjoint and whose distribution, from the learner's point of view, is still non-stationary. Our results show that dedicated CL methods can significantly improve learning when compared to the baseline technique of "experience replay".

An Investigation of Replay-based Approaches for Continual Learning

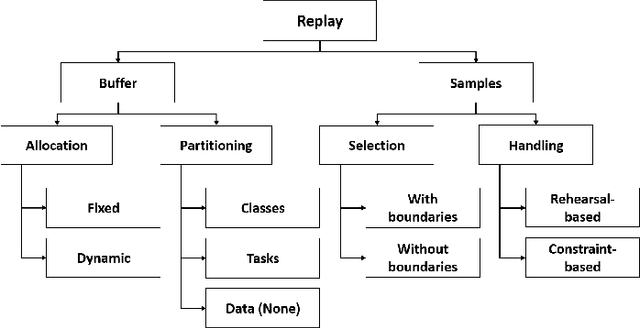
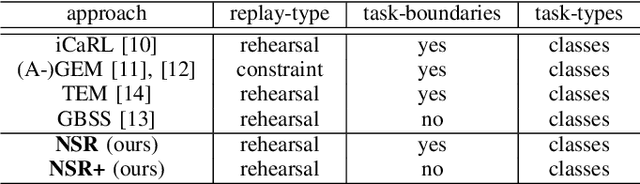
Continual learning (CL) is a major challenge of machine learning (ML) and describes the ability to learn several tasks sequentially without catastrophic forgetting (CF). Recent works indicate that CL is a complex topic, even more so when real-world scenarios with multiple constraints are involved. Several solution classes have been proposed, of which so-called replay-based approaches seem very promising due to their simplicity and robustness. Such approaches store a subset of past samples in a dedicated memory for later processing: while this does not solve all problems, good results have been obtained. In this article, we empirically investigate replay-based approaches of continual learning and assess their potential for applications. Selected recent approaches as well as own proposals are compared on a common set of benchmarks, with a particular focus on assessing the performance of different sample selection strategies. We find that the impact of sample selection increases when a smaller number of samples is stored. Nevertheless, performance varies strongly between different replay approaches. Surprisingly, we find that the most naive rehearsal-based approaches that we propose here can outperform recent state-of-the-art methods.

Continual Learning with Fully Probabilistic Models

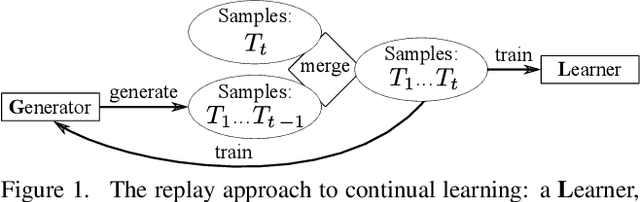
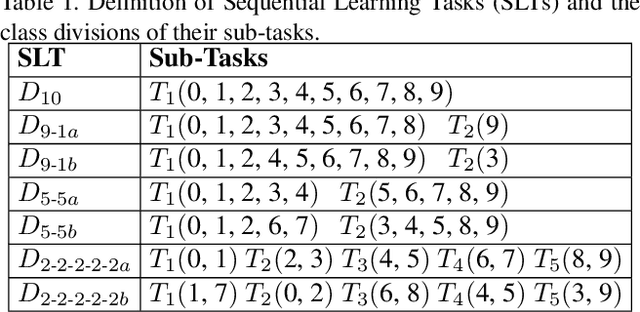
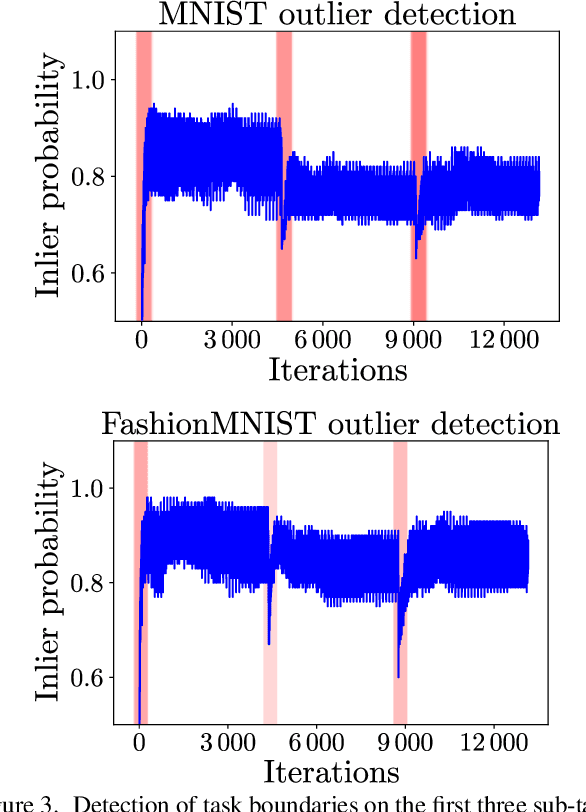
We present an approach for continual learning (CL) that is based on fully probabilistic (or generative) models of machine learning. In contrast to, e.g., GANs that are "generative" in the sense that they can generate samples, fully probabilistic models aim at modeling the data distribution directly. Consequently, they provide functionalities that are highly relevant for continual learning, such as density estimation (outlier detection) and sample generation. As a concrete realization of generative continual learning, we propose Gaussian Mixture Replay (GMR). GMR is a pseudo-rehearsal approach using a Gaussian Mixture Model (GMM) instance for both generator and classifier functionalities. Relying on the MNIST, FashionMNIST and Devanagari benchmarks, we first demonstrate unsupervised task boundary detection by GMM density estimation, which we also use to reject untypical generated samples. In addition, we show that GMR is capable of class-conditional sampling in the way of a cGAN. Lastly, we verify that GMR, despite its simple structure, achieves state-of-the-art performance on common class-incremental learning problems at very competitive time and memory complexity.