Weighted MCC: A Robust Measure of Multiclass Classifier Performance for Observations with Individual Weights

Several performance measures are used to evaluate binary and multiclass classification tasks. But individual observations may often have distinct weights, and none of these measures are sensitive to such varying weights. We propose a new weighted Pearson-Matthews Correlation Coefficient (MCC) for binary classification as well as weighted versions of related multiclass measures. The weighted MCC varies between $-1$ and $1$. But crucially, the weighted MCC values are higher for classifiers that perform better on highly weighted observations, and hence is able to distinguish them from classifiers that have a similar overall performance and ones that perform better on the lowly weighted observations. Furthermore, we prove that the weighted measures are robust with respect to the choice of weights in a precise manner: if the weights are changed by at most $ε$, the value of the weighted measure changes at most by a factor of $ε$ in the binary case and by a factor of $ε^2$ in the multiclass case. Our computations demonstrate that the weighted measures clearly identify classifiers that perform better on higher weighted observations, while the unweighted measures remain completely indifferent to the choices of weights.

Dynamic Learning Rate Scheduling based on Loss Changes Leads to Faster Convergence

Despite significant advances in optimizers for training, most research works use common scheduler choices like Cosine or exponential decay. In this paper, we study \emph{GreedyLR}, a novel scheduler that adaptively adjusts the learning rate during training based on the current loss. To validate the effectiveness of our proposed scheduler, we conduct experiments on several NLP, CV, and LLM tasks with up to $7B$ parameters, including both fine-tuning and pre-training experiments. The results show that our approach outperforms several state-of-the-art schedulers in terms of accuracy, speed, and convergence. We also provide a theoretical analysis of the GreedyLR algorithm, including a proof of convergence and derivation of the optimal scaling factor $F$ that maximizes the convergence rate, along with experiments to show robustness of the algorithm to realistic noisy landscapes. Our scheduler is easy to implement, computationally efficient, and could be considered a good default scheduler for training.

A Stable Measure for Conditional Periodicity of Time Series using Persistent Homology

Given a pair of time series, we study how the periodicity of one influences the periodicity of the other. There are several known methods to measure the similarity between a pair of time series, such as cross-correlation, coherence, cross-recurrence, and dynamic time warping. But we have yet to find any measures with theoretical stability results. Persistence homology has been utilized to construct a scoring function with theoretical guarantees of stability that quantifies the periodicity of a single univariate time series f1, denoted score(f1). Building on this concept, we propose a conditional periodicity score that quantifies the periodicity of one univariate time series f1 given another f2, denoted score(f1|f2), and derive theoretical stability results for the same. With the use of dimension reduction in mind, we prove a new stability result for score(f1|f2) under principal component analysis (PCA) when we use the projections of the time series embeddings onto their respective first K principal components. We show that the change in our score is bounded by a function of the eigenvalues corresponding to the remaining (unused) N-K principal components and hence is small when the first K principal components capture most of the variation in the time series embeddings. Finally we derive a lower bound on the minimum embedding dimension to use in our pipeline which guarantees that any two such embeddings give scores that are within a given epsilon of each other. We present a procedure for computing conditional periodicity scores and implement it on several pairs of synthetic signals. We experimentally compare our similarity measure to the most-similar statistical measure of cross-recurrence, and show the increased accuracy and stability of our score when predicting and measuring whether or not the periodicities of two time series are similar.

Learning to Simulate Aerosol Dynamics with Graph Neural Networks

Aerosol effects on climate, weather, and air quality depend on characteristics of individual particles, which are tremendously diverse and change in time. Particle-resolved models are the only models able to capture this diversity in particle physiochemical properties, and these models are computationally expensive. As a strategy for accelerating particle-resolved microphysics models, we introduce Graph-based Learning of Aerosol Dynamics (GLAD) and use this model to train a surrogate of the particle-resolved model PartMC-MOSAIC. GLAD implements a Graph Network-based Simulator (GNS), a machine learning framework that has been used to simulate particle-based fluid dynamics models. In GLAD, each particle is represented as a node in a graph, and the evolution of the particle population over time is simulated through learned message passing. We demonstrate our GNS approach on a simple aerosol system that includes condensation of sulfuric acid onto particles composed of sulfate, black carbon, organic carbon, and water. A graph with particles as nodes is constructed, and a graph neural network (GNN) is then trained using the model output from PartMC-MOSAIC. The trained GNN can then be used for simulating and predicting aerosol dynamics over time. Results demonstrate the framework's ability to accurately learn chemical dynamics and generalize across different scenarios, achieving efficient training and prediction times. We evaluate the performance across three scenarios, highlighting the framework's robustness and adaptability in modeling aerosol microphysics and chemistry.

Predictive Analytics of Varieties of Potatoes

We explore the application of machine learning algorithms to predict the suitability of Russet potato clones for advancement in breeding trials. Leveraging data from manually collected trials in the state of Oregon, we investigate the potential of a wide variety of state-of-the-art binary classification models. We conduct a comprehensive analysis of the dataset that includes preprocessing, feature engineering, and imputation to address missing values. We focus on several key metrics such as accuracy, F1-score, and Matthews correlation coefficient (MCC) for model evaluation. The top-performing models, namely the multi-layer perceptron (MLPC), histogram-based gradient boosting classifier (HGBC), and a support vector machine (SVC), demonstrate consistent and significant results. Variable selection further enhances model performance and identifies influential features in predicting trial outcomes. The findings emphasize the potential of machine learning in streamlining the selection process for potato varieties, offering benefits such as increased efficiency, substantial cost savings, and judicious resource utilization. Our study contributes insights into precision agriculture and showcases the relevance of advanced technologies for informed decision-making in breeding programs.

A Normalized Bottleneck Distance on Persistence Diagrams and Homology Preservation under Dimension Reduction

Persistence diagrams are used as signatures of point cloud data assumed to be sampled from manifolds, and represent their topology in a compact fashion. Further, two given clouds of points can be compared by directly comparing their persistence diagrams using the bottleneck distance, d_B. But one potential drawback of this pipeline is that point clouds sampled from topologically similar manifolds can have arbitrarily large d_B values when there is a large degree of scaling between them. This situation is typical in dimension reduction frameworks that are also aiming to preserve topology. We define a new scale-invariant distance between persistence diagrams termed normalized bottleneck distance, d_N, and study its properties. In defining d_N, we also develop a broader framework called metric decomposition for comparing finite metric spaces of equal cardinality with a bijection. We utilize metric decomposition to prove a stability result for d_N by deriving an explicit bound on the distortion of the associated bijective map. We then study two popular dimension reduction techniques, Johnson-Lindenstrauss (JL) projections and metric multidimensional scaling (mMDS), and a third class of general biLipschitz mappings. We provide new bounds on how well these dimension reduction techniques preserve homology with respect to d_N. For a JL map f that transforms input X to f(X), we show that d_N(dgm(X),dgm(f(X)) < e, where dgm(X) is the Vietoris-Rips persistence diagram of X, and 0 < e < 1 is the tolerance up to which pairwise distances are preserved by f. For mMDS, we present new bounds for both d_B and d_N between persistence diagrams of X and its projection in terms of the eigenvalues of the covariance matrix. And for k-biLipschitz maps, we show that d_N is bounded by the product of (k^2-1)/k and the ratio of diameters of X and f(X).

Continuous Toolpath Planning in Additive Manufacturing

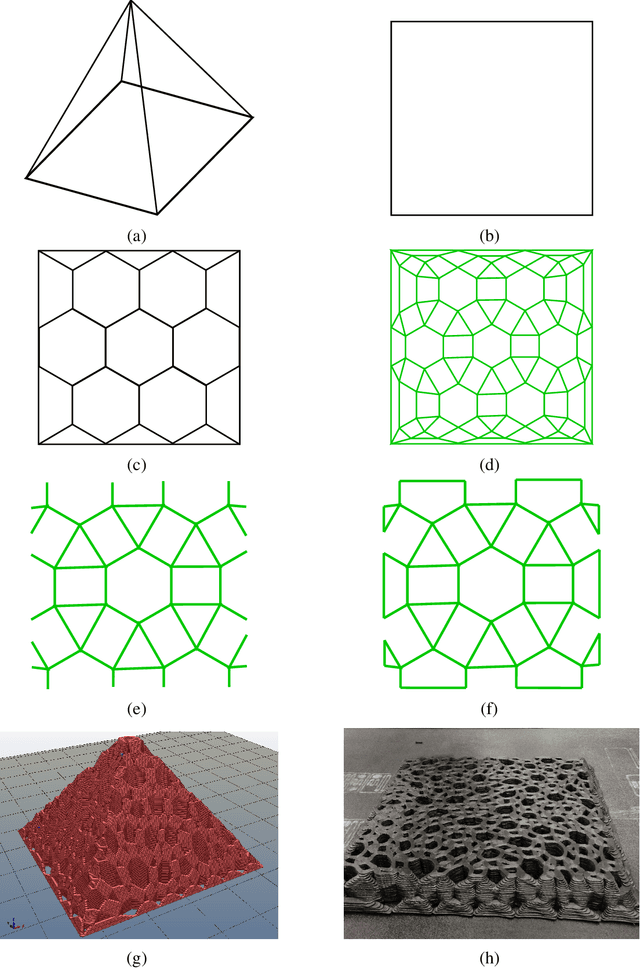
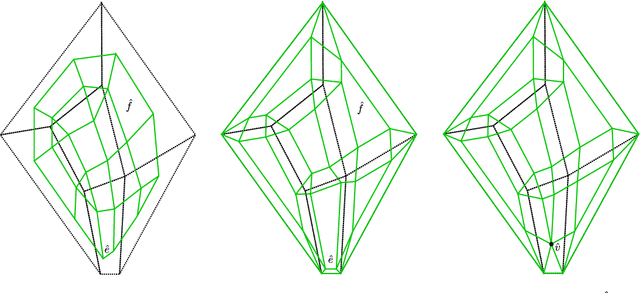
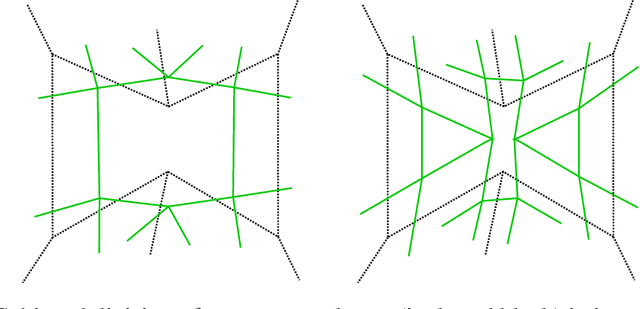
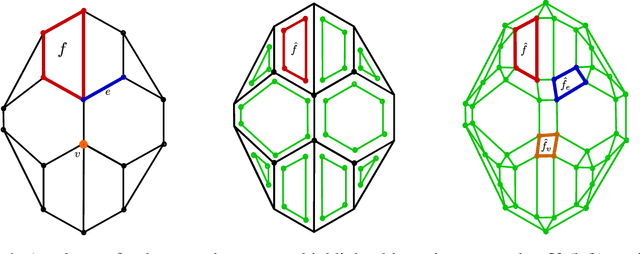
We develop a framework that creates a new polygonal mesh representation of the 3D domain of a layer-by-layer 3D printing job on which we identify single, continuous tool paths covering each connected piece of the domain in every layer. We present a tool path algorithm that traverses each such continuous tool path with no crossovers. The key construction at the heart of our framework is a novel Euler transformation that we introduced recently in a separate manuscript. Our Euler transformation converts a 2-dimensional cell complex K into a new 2-complex K^ such that every vertex in the 1-skeleton G^ of K^ has degree 4. Hence G^ is Eulerian, and an Eulerian tour can be followed to print all edges in a continuous fashion without stops. We start with a mesh K of the union of polygons obtained by projecting all layers to the plane. First we compute its Euler transformation K^. In the slicing step, we clip K^ at each layer i using its polygon to obtain K^_i. We then patch K^_i by adding edges such that any odd-degree nodes created by slicing are transformed to have even degrees again. We print extra support edges in place of any segments left out to ensure there are no edges without support in the next layer above. These support edges maintain the Euler nature of K^_i. Finally, we describe a tree-based search algorithm that builds the continuous tool path by traversing "concentric" cycles in the Euler complex. Our algorithm produces a tool path that avoids material collisions and crossovers, and can be printed in a continuous fashion irrespective of complex geometry or topology of the domain (e.g., holes).

Jaccard Filtration and Stable Paths in the Mapper

The contributions of this paper are two-fold. We define a new filtration called the cover filtration built from a single cover based on a generalized Jaccard distance. We provide stability results for the cover filtration and show how the construction is equivalent to the Cech filtration under certain settings. We then develop a language and theory for stable paths within this filtration, inspired by ideas of persistent homology. We demonstrate how the filtration and paths can be applied to a variety of applications in which defining a metric is not obvious but a cover is readily available. We demonstrate the usefulness of this construction by employing it in the context of recommendation systems and explainable machine learning. We demonstrate a new perspective for modeling recommendation system data sets that does not require manufacturing a bespoke metric. This extends work on graph-based recommendation systems, allowing a topological perspective. For an explicit example, we look at a movies data set and we find the stable paths identified in our framework represent a sequence of movies constituting a gentle transition and ordering from one genre to another. For explainable machine learning, we apply the Mapper for model induction, providing explanations in the form of paths between subpopulations or observations. Our framework provides an alternative way of building a filtration from a single mapper that is then used to explore stable paths. As a direct illustration, we build a mapper from a supervised machine learning model trained on the FashionMNIST data set. We show that the stable paths in the cover filtration provide improved explanations of relationships between subpopulations of images.