Elizabeth P. Thompson
A Stable Measure for Conditional Periodicity of Time Series using Persistent Homology
Jan 06, 2025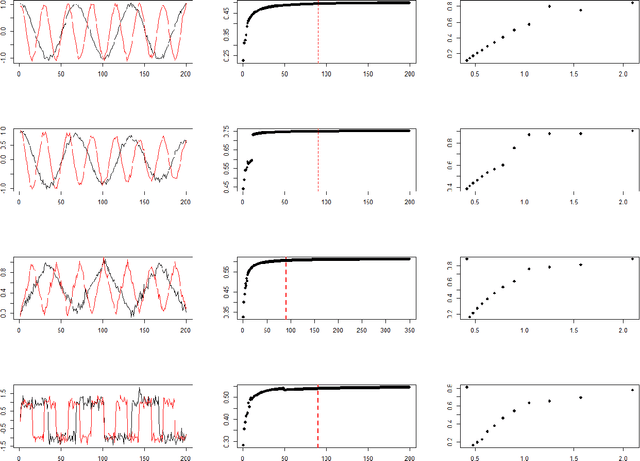
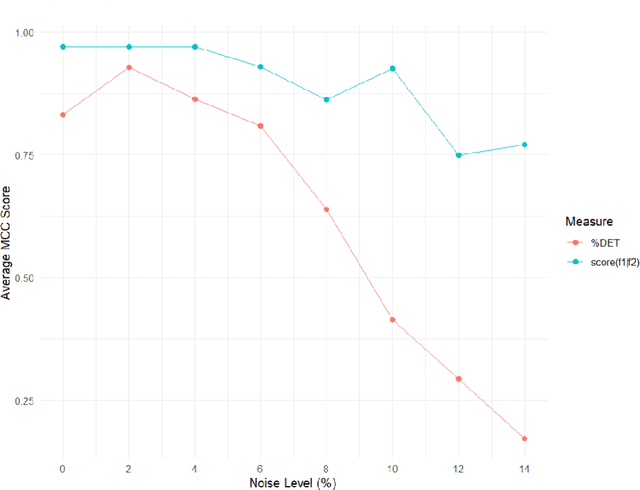
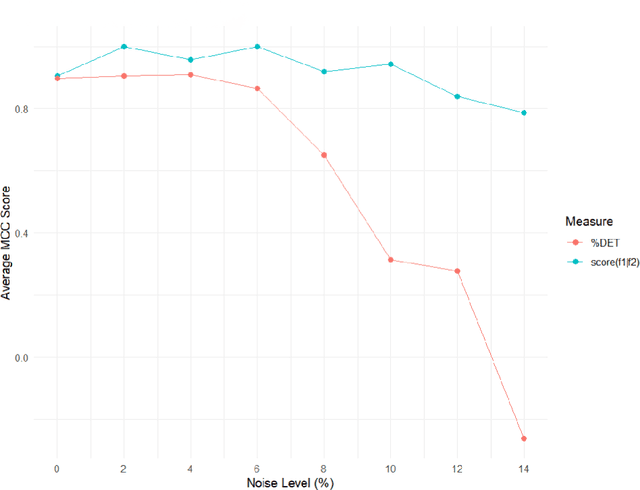
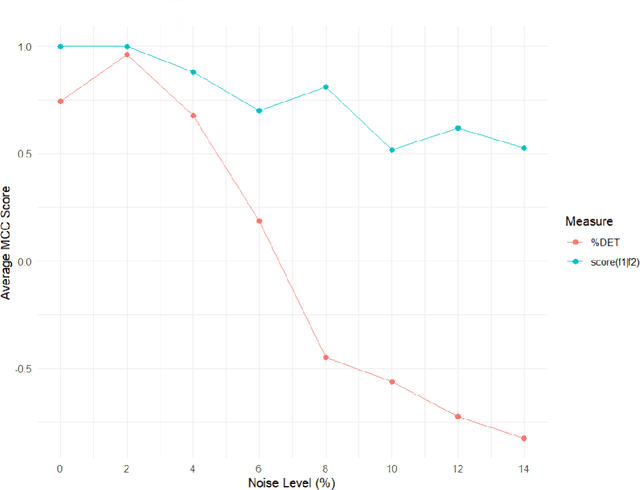
Abstract:Given a pair of time series, we study how the periodicity of one influences the periodicity of the other. There are several known methods to measure the similarity between a pair of time series, such as cross-correlation, coherence, cross-recurrence, and dynamic time warping. But we have yet to find any measures with theoretical stability results. Persistence homology has been utilized to construct a scoring function with theoretical guarantees of stability that quantifies the periodicity of a single univariate time series f1, denoted score(f1). Building on this concept, we propose a conditional periodicity score that quantifies the periodicity of one univariate time series f1 given another f2, denoted score(f1|f2), and derive theoretical stability results for the same. With the use of dimension reduction in mind, we prove a new stability result for score(f1|f2) under principal component analysis (PCA) when we use the projections of the time series embeddings onto their respective first K principal components. We show that the change in our score is bounded by a function of the eigenvalues corresponding to the remaining (unused) N-K principal components and hence is small when the first K principal components capture most of the variation in the time series embeddings. Finally we derive a lower bound on the minimum embedding dimension to use in our pipeline which guarantees that any two such embeddings give scores that are within a given epsilon of each other. We present a procedure for computing conditional periodicity scores and implement it on several pairs of synthetic signals. We experimentally compare our similarity measure to the most-similar statistical measure of cross-recurrence, and show the increased accuracy and stability of our score when predicting and measuring whether or not the periodicities of two time series are similar.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge