Communication Optimization in Large Scale Federated Learning using Autoencoder Compressed Weight Updates

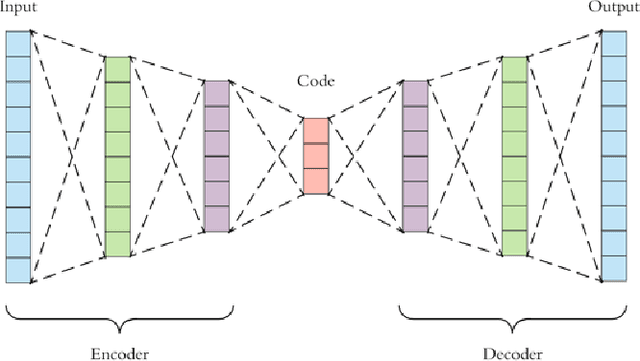
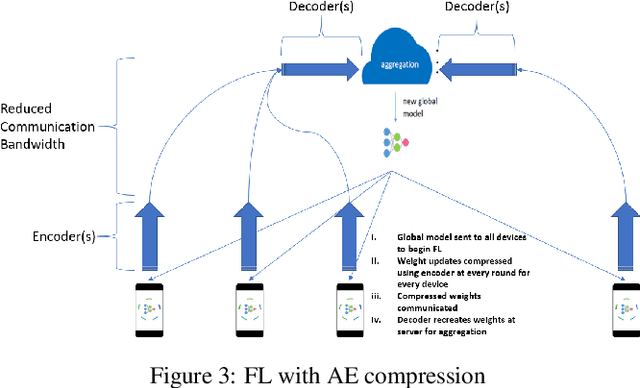
Federated Learning (FL) solves many of this decade's concerns regarding data privacy and computation challenges. FL ensures no data leaves its source as the model is trained at where the data resides. However, FL comes with its own set of challenges. The communication of model weight updates in this distributed environment comes with significant network bandwidth costs. In this context, we propose a mechanism of compressing the weight updates using Autoencoders (AE), which learn the data features of the weight updates and subsequently perform compression. The encoder is set up on each of the nodes where the training is performed while the decoder is set up on the node where the weights are aggregated. This setup achieves compression through the encoder and recreates the weights at the end of every communication round using the decoder. This paper shows that the dynamic and orthogonal AE based weight compression technique could serve as an advantageous alternative (or an add-on) in a large scale FL, as it not only achieves compression ratios ranging from 500x to 1720x and beyond, but can also be modified based on the accuracy requirements, computational capacity, and other requirements of the given FL setup.

Weight Divergence Driven Divide-and-Conquer Approach for Optimal Federated Learning from non-IID Data

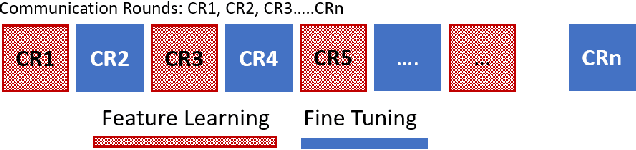
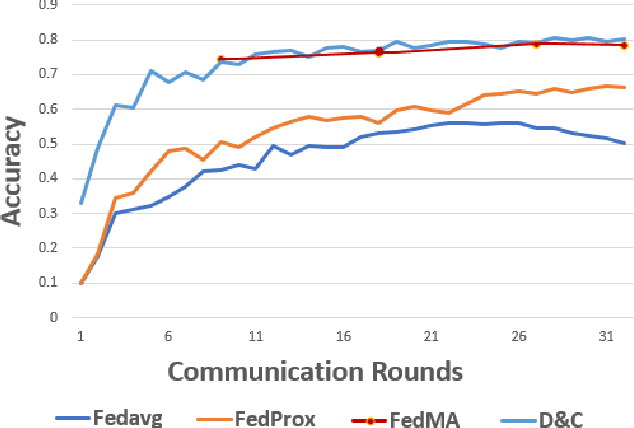
Federated Learning allows training of data stored in distributed devices without the need for centralizing training data, thereby maintaining data privacy. Addressing the ability to handle data heterogeneity (non-identical and independent distribution or non-IID) is a key enabler for the wider deployment of Federated Learning. In this paper, we propose a novel Divide-and-Conquer training methodology that enables the use of the popular FedAvg aggregation algorithm by overcoming the acknowledged FedAvg limitations in non-IID environments. We propose a novel use of Cosine-distance based Weight Divergence metric to determine the exact point where a Deep Learning network can be divided into class agnostic initial layers and class-specific deep layers for performing a Divide and Conquer training. We show that the methodology achieves trained model accuracy at par (and in certain cases exceeding) with numbers achieved by state-of-the-art Aggregation algorithms like FedProx, FedMA, etc. Also, we show that this methodology leads to compute and bandwidth optimizations under certain documented conditions.