Predictive Sampling with Forecasting Autoregressive Models

Autoregressive models (ARMs) currently hold state-of-the-art performance in likelihood-based modeling of image and audio data. Generally, neural network based ARMs are designed to allow fast inference, but sampling from these models is impractically slow. In this paper, we introduce the predictive sampling algorithm: a procedure that exploits the fast inference property of ARMs in order to speed up sampling, while keeping the model intact. We propose two variations of predictive sampling, namely sampling with ARM fixed-point iteration and learned forecasting modules. Their effectiveness is demonstrated in two settings: i) explicit likelihood modeling on binary MNIST, SVHN and CIFAR10, and ii) discrete latent modeling in an autoencoder trained on SVHN, CIFAR10 and Imagenet32. Empirically, we show considerable improvements over baselines in number of ARM inference calls and sampling speed.

Risk-averse Behavior Planning for Autonomous Driving under Uncertainty

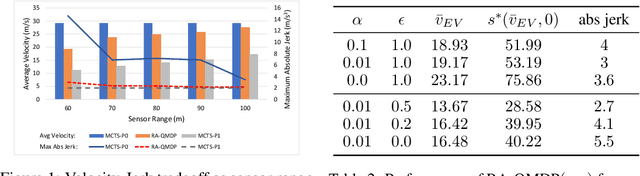
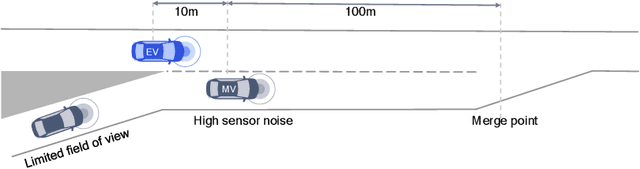
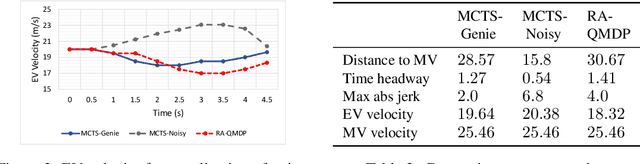
Autonomous vehicles have to navigate the surrounding environment with partial observability of other objects sharing the road. Sources of uncertainty in autonomous vehicle measurements include sensor fusion errors, limited sensor range due to weather or object detection latency, occlusion, and hidden parameters such as other human driver intentions. Behavior planning must consider all sources of uncertainty in deciding future vehicle maneuvers. This paper presents a scalable framework for risk-averse behavior planning under uncertainty by incorporating QMDP, unscented transform, and Monte Carlo tree search (MCTS). It is shown that upper confidence bound (UCB) for expanding the tree results in noisy Q-value estimates by the MCTS and a degraded performance of QMDP. A modification to action selection procedure in MCTS is proposed to achieve robust performance.

Structure in the Value Function of Two-Player Zero-Sum Games of Incomplete Information

Zero-sum stochastic games provide a rich model for competitive decision making. However, under general forms of state uncertainty as considered in the Partially Observable Stochastic Game (POSG), such decision making problems are still not very well understood. This paper makes a contribution to the theory of zero-sum POSGs by characterizing structure in their value function. In particular, we introduce a new formulation of the value function for zs-POSGs as a function of the "plan-time sufficient statistics" (roughly speaking the information distribution in the POSG), which has the potential to enable generalization over such information distributions. We further delineate this generalization capability by proving a structural result on the shape of value function: it exhibits concavity and convexity with respect to appropriately chosen marginals of the statistic space. This result is a key pre-cursor for developing solution methods that may be able to exploit such structure. Finally, we show how these results allow us to reduce a zs-POSG to a "centralized" model with shared observations, thereby transferring results for the latter, narrower class, to games with individual (private) observations.