Audun Josang
Active Learning on Neural Networks through Interactive Generation of Digit Patterns and Visual Representation
Oct 02, 2023



Abstract:Artificial neural networks (ANNs) have been broadly utilized to analyze various data and solve different domain problems. However, neural networks (NNs) have been considered a black box operation for years because their underlying computation and meaning are hidden. Due to this nature, users often face difficulties in interpreting the underlying mechanism of the NNs and the benefits of using them. In this paper, to improve users' learning and understanding of NNs, an interactive learning system is designed to create digit patterns and recognize them in real time. To help users clearly understand the visual differences of digit patterns (i.e., 0 ~ 9) and their results with an NN, integrating visualization is considered to present all digit patterns in a two-dimensional display space with supporting multiple user interactions. An evaluation with multiple datasets is conducted to determine its usability for active learning. In addition, informal user testing is managed during a summer workshop by asking the workshop participants to use the system.
Cumulative and Averaging Fission of Beliefs
Dec 07, 2007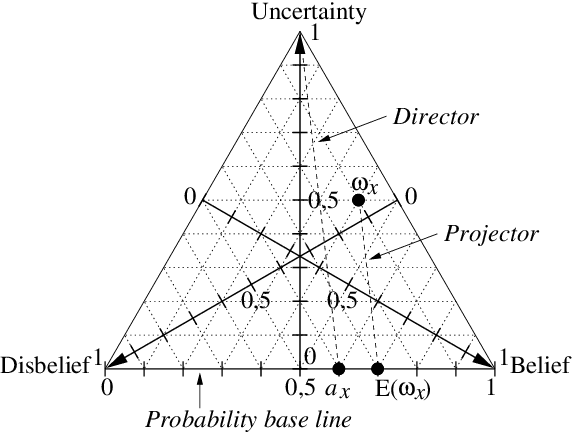
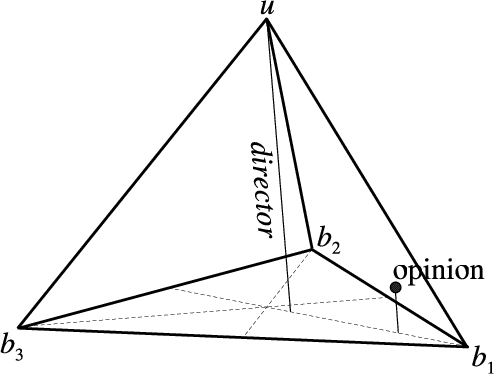
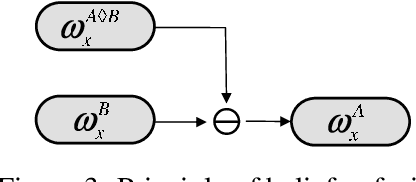
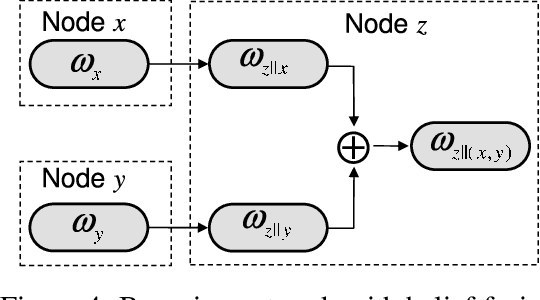
Abstract:Belief fusion is the principle of combining separate beliefs or bodies of evidence originating from different sources. Depending on the situation to be modelled, different belief fusion methods can be applied. Cumulative and averaging belief fusion is defined for fusing opinions in subjective logic, and for fusing belief functions in general. The principle of fission is the opposite of fusion, namely to eliminate the contribution of a specific belief from an already fused belief, with the purpose of deriving the remaining belief. This paper describes fission of cumulative belief as well as fission of averaging belief in subjective logic. These operators can for example be applied to belief revision in Bayesian belief networks, where the belief contribution of a given evidence source can be determined as a function of a given fused belief and its other contributing beliefs.
The Cumulative Rule for Belief Fusion
Jun 14, 2006Abstract:The problem of combining beliefs in the Dempster-Shafer belief theory has attracted considerable attention over the last two decades. The classical Dempster's Rule has often been criticised, and many alternative rules for belief combination have been proposed in the literature. The consensus operator for combining beliefs has nice properties and produces more intuitive results than Dempster's rule, but has the limitation that it can only be applied to belief distribution functions on binary state spaces. In this paper we present a generalisation of the consensus operator that can be applied to Dirichlet belief functions on state spaces of arbitrary size. This rule, called the cumulative rule of belief combination, can be derived from classical statistical theory, and corresponds well with human intuition.
Belief Calculus
Jun 07, 2006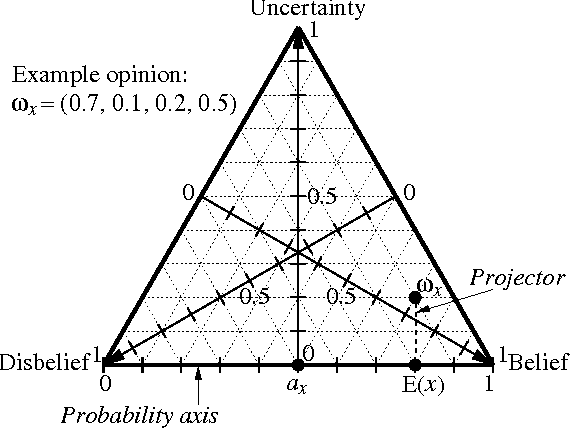

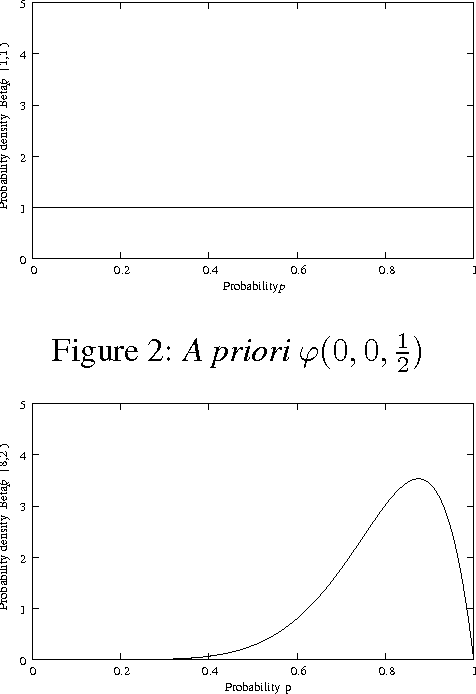
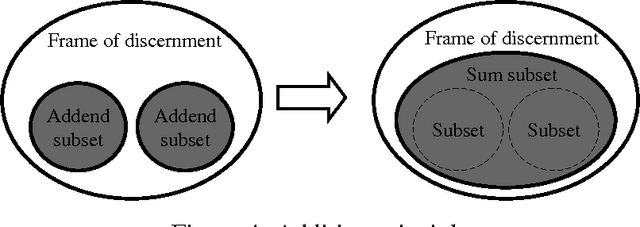
Abstract:In Dempster-Shafer belief theory, general beliefs are expressed as belief mass distribution functions over frames of discernment. In Subjective Logic beliefs are expressed as belief mass distribution functions over binary frames of discernment. Belief representations in Subjective Logic, which are called opinions, also contain a base rate parameter which express the a priori belief in the absence of evidence. Philosophically, beliefs are quantitative representations of evidence as perceived by humans or by other intelligent agents. The basic operators of classical probability calculus, such as addition and multiplication, can be applied to opinions, thereby making belief calculus practical. Through the equivalence between opinions and Beta probability density functions, this also provides a calculus for Beta probability density functions. This article explains the basic elements of belief calculus.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge