Efficiency of First-Order Methods for Low-Rank Tensor Recovery with the Tensor Nuclear Norm Under Strict Complementarity

We consider convex relaxations for recovering low-rank tensors based on constrained minimization over a ball induced by the tensor nuclear norm, recently introduced in \cite{tensor_tSVD}. We build on a recent line of results that considered convex relaxations for the recovery of low-rank matrices and established that under a strict complementarity condition (SC), both the convergence rate and per-iteration runtime of standard gradient methods may improve dramatically. We develop the appropriate strict complementarity condition for the tensor nuclear norm ball and obtain the following main results under this condition: 1. When the objective to minimize is of the form $f(\mX)=g(\mA\mX)+\langle{\mC,\mX}\rangle$ , where $g$ is strongly convex and $\mA$ is a linear map (e.g., least squares), a quadratic growth bound holds, which implies linear convergence rates for standard projected gradient methods, despite the fact that $f$ need not be strongly convex. 2. For a smooth objective function, when initialized in certain proximity of an optimal solution which satisfies SC, standard projected gradient methods only require SVD computations (for projecting onto the tensor nuclear norm ball) of rank that matches the tubal rank of the optimal solution. In particular, when the tubal rank is constant, this implies nearly linear (in the size of the tensor) runtime per iteration, as opposed to super linear without further assumptions. 3. For a nonsmooth objective function which admits a popular smooth saddle-point formulation, we derive similar results to the latter for the well known extragradient method. An additional contribution which may be of independent interest, is the rigorous extension of many basic results regarding tensors of arbitrary order, which were previously obtained only for third-order tensors.

Low-Rank Mirror-Prox for Nonsmooth and Low-Rank Matrix Optimization Problems

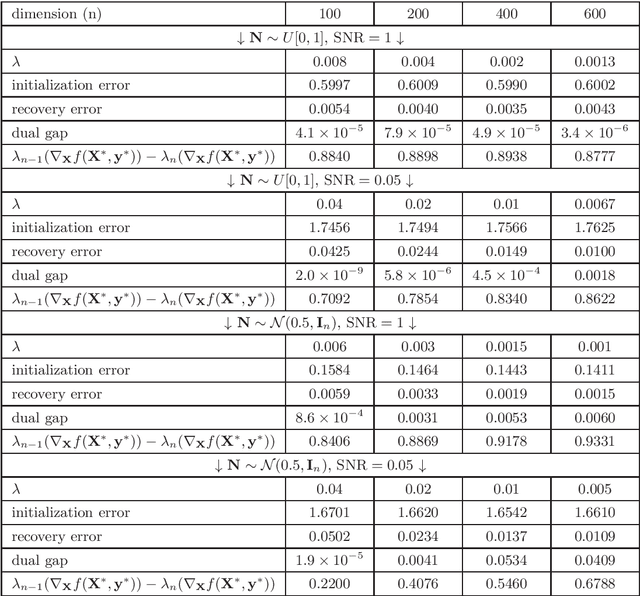
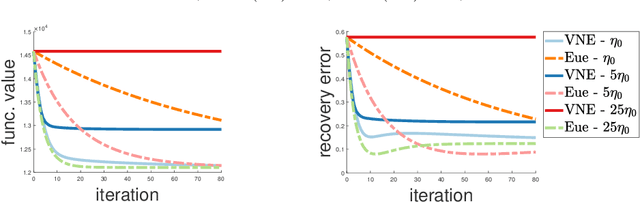
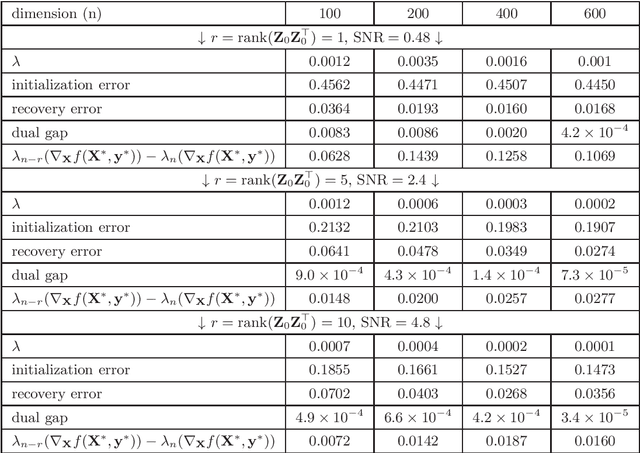
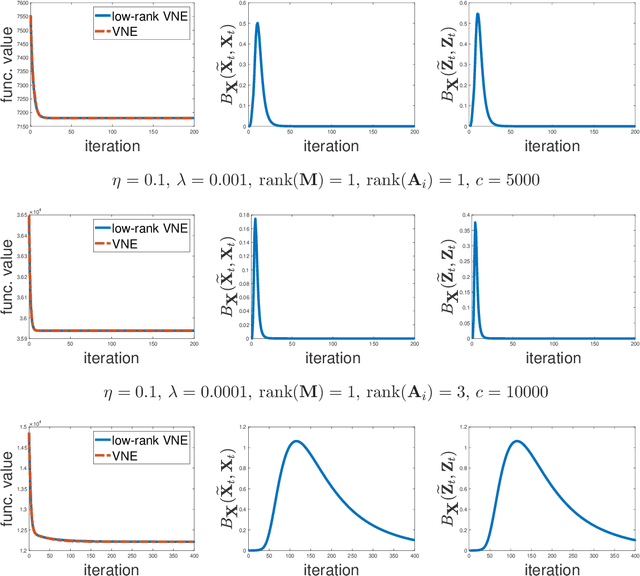
Low-rank and nonsmooth matrix optimization problems capture many fundamental tasks in statistics and machine learning. While significant progress has been made in recent years in developing efficient methods for \textit{smooth} low-rank optimization problems that avoid maintaining high-rank matrices and computing expensive high-rank SVDs, advances for nonsmooth problems have been slow paced. In this paper we consider standard convex relaxations for such problems. Mainly, we prove that under a \textit{strict complementarity} condition and under the relatively mild assumption that the nonsmooth objective can be written as a maximum of smooth functions, approximated variants of two popular \textit{mirror-prox} methods: the Euclidean \textit{extragradient method} and mirror-prox with \textit{matrix exponentiated gradient updates}, when initialized with a "warm-start", converge to an optimal solution with rate $O(1/t)$, while requiring only two \textit{low-rank} SVDs per iteration. Moreover, for the extragradient method we also consider relaxed versions of strict complementarity which yield a trade-off between the rank of the SVDs required and the radius of the ball in which we need to initialize the method. We support our theoretical results with empirical experiments on several nonsmooth low-rank matrix recovery tasks, demonstrating both the plausibility of the strict complementarity assumption, and the efficient convergence of our proposed low-rank mirror-prox variants.

Low-Rank Extragradient Method for Nonsmooth and Low-Rank Matrix Optimization Problems

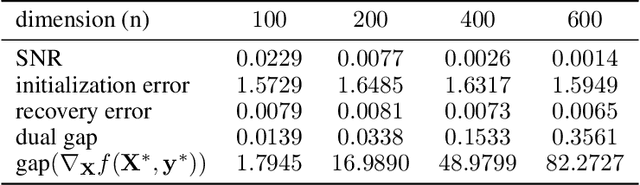
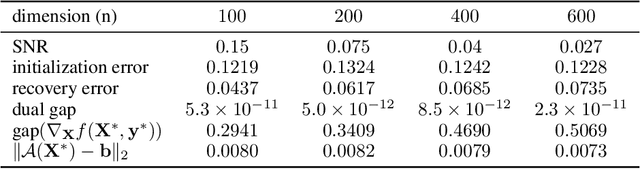
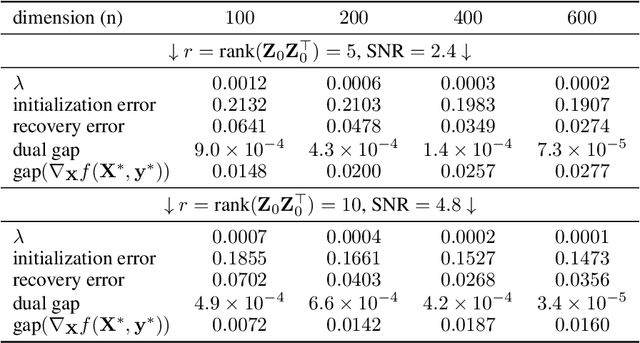
Low-rank and nonsmooth matrix optimization problems capture many fundamental tasks in statistics and machine learning. While significant progress has been made in recent years in developing efficient methods for \textit{smooth} low-rank optimization problems that avoid maintaining high-rank matrices and computing expensive high-rank SVDs, advances for nonsmooth problems have been slow paced. In this paper we consider standard convex relaxations for such problems. Mainly, we prove that under a natural \textit{generalized strict complementarity} condition and under the relatively mild assumption that the nonsmooth objective can be written as a maximum of smooth functions, the \textit{extragradient method}, when initialized with a "warm-start" point, converges to an optimal solution with rate $O(1/t)$ while requiring only two \textit{low-rank} SVDs per iteration. We give a precise trade-off between the rank of the SVDs required and the radius of the ball in which we need to initialize the method. We support our theoretical results with empirical experiments on several nonsmooth low-rank matrix recovery tasks, demonstrating that using simple initializations, the extragradient method produces exactly the same iterates when full-rank SVDs are replaced with SVDs of rank that matches the rank of the (low-rank) ground-truth matrix to be recovered.

On the Efficient Implementation of the Matrix Exponentiated Gradient Algorithm for Low-Rank Matrix Optimization

Convex optimization over the spectrahedron, i.e., the set of all real $n\times n$ positive semidefinite matrices with unit trace, has important applications in machine learning, signal processing and statistics, mainly as a convex relaxation for optimization with low-rank matrices. It is also one of the most prominent examples in the theory of first-order methods for convex optimization in which non-Euclidean methods can be significantly preferable to their Euclidean counterparts, and in particular the Matrix Exponentiated Gradient (MEG) method which is based on the Bregman distance induced by the (negative) von Neumann entropy. Unfortunately, implementing MEG requires a full SVD computation on each iteration, which is not scalable to high-dimensional problems. In this work we propose efficient implementations of MEG, both with deterministic and stochastic gradients, which are tailored for optimization with low-rank matrices, and only use a single low-rank SVD computation on each iteration. We also provide efficiently-computable certificates for the correct convergence of our methods. Mainly, we prove that under a strict complementarity condition, the suggested methods converge from a "warm-start" initialization with similar rates to their full-SVD-based counterparts. Finally, we bring empirical experiments which both support our theoretical findings and demonstrate the practical appeal of our methods.

Fast Stochastic Algorithms for Low-rank and Nonsmooth Matrix Problems

Composite convex optimization problems which include both a nonsmooth term and a low-rank promoting term have important applications in machine learning and signal processing, such as when one wishes to recover an unknown matrix that is simultaneously low-rank and sparse. However, such problems are highly challenging to solve in large-scale: the low-rank promoting term prohibits efficient implementations of proximal methods for composite optimization and even simple subgradient methods. On the other hand, methods which are tailored for low-rank optimization, such as conditional gradient-type methods, which are often applied to a smooth approximation of the nonsmooth objective, are slow since their runtime scales with both the large Lipshitz parameter of the smoothed gradient vector and with $1/\epsilon$. In this paper we develop efficient algorithms for \textit{stochastic} optimization of a strongly-convex objective which includes both a nonsmooth term and a low-rank promoting term. In particular, to the best of our knowledge, we present the first algorithm that enjoys all following critical properties for large-scale problems: i) (nearly) optimal sample complexity, ii) each iteration requires only a single \textit{low-rank} SVD computation, and iii) overall number of thin-SVD computations scales only with $\log{1/\epsilon}$ (as opposed to $\textrm{poly}(1/\epsilon)$ in previous methods). We also give an algorithm for the closely-related finite-sum setting. At the heart of our results lie a novel combination of a variance-reduction technique and the use of a \textit{weak-proximal oracle} which is key to obtaining all above three properties simultaneously.

Fast Generalized Conditional Gradient Method with Applications to Matrix Recovery Problems

Motivated by matrix recovery problems such as Robust Principal Component Analysis, we consider a general optimization problem of minimizing a smooth and strongly convex loss applied to the sum of two blocks of variables, where each block of variables is constrained or regularized individually. We present a novel Generalized Conditional Gradient method which is able to leverage the special structure of the problem to obtain faster convergence rates than those attainable via standard methods, under a variety of interesting assumptions. In particular, our method is appealing for matrix problems in which one of the blocks corresponds to a low-rank matrix and avoiding prohibitive full-rank singular value decompositions, which are required by most standard methods, is most desirable. Importantly, while our initial motivation comes from problems which originated in statistics, our analysis does not impose any statistical assumptions on the data.