Scene-VLM: Multimodal Video Scene Segmentation via Vision-Language Models

Segmenting long-form videos into semantically coherent scenes is a fundamental task in large-scale video understanding. Existing encoder-based methods are limited by visual-centric biases, classify each shot in isolation without leveraging sequential dependencies, and lack both narrative understanding and explainability. In this paper, we present Scene-VLM, the first fine-tuned vision-language model (VLM) framework for video scene segmentation. Scene-VLM jointly processes visual and textual cues including frames, transcriptions, and optional metadata to enable multimodal reasoning across consecutive shots. The model generates predictions sequentially with causal dependencies among shots and introduces a context-focus window mechanism to ensure sufficient temporal context for each shot-level decision. In addition, we propose a scheme to extract confidence scores from the token-level logits of the VLM, enabling controllable precision-recall trade-offs that were previously limited to encoder-based methods. Furthermore, we demonstrate that our model can be aligned to generate coherent natural-language rationales for its boundary decisions through minimal targeted supervision. Our approach achieves state-of-the-art performance on standard scene segmentation benchmarks. On MovieNet, for example, Scene-VLM yields significant improvements of +6 AP and +13.7 F1 over the previous leading method.

Group-Aware Reinforcement Learning for Output Diversity in Large Language Models

Large Language Models (LLMs) often suffer from mode collapse, repeatedly generating the same few completions even when many valid answers exist, limiting their diversity across a wide range of tasks. We introduce Group-Aware Policy Optimization (GAPO), a simple extension of the recent and popular Group Relative Policy Optimization (GRPO) that computes rewards over the group as a whole. GAPO enables learning from the group-level properties such as diversity and coverage. We demonstrate GAPO using a frequency-aware reward function that encourages uniform sampling over valid LLM completions, and show that GAPO-trained models produce valid and more diverse model responses. Beyond this setup, GAPO generalizes to open-ended prompts and improves response diversity without compromising accuracy on standard LLM benchmarks (GSM8K, MATH, HumanEval, MMLU-Pro). Our code will be made publicly available.

Conformal Prediction is Robust to Label Noise

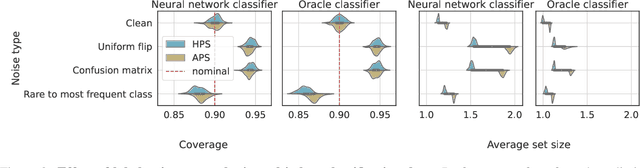
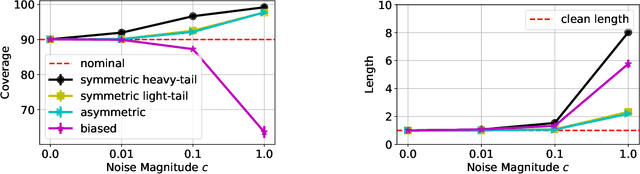
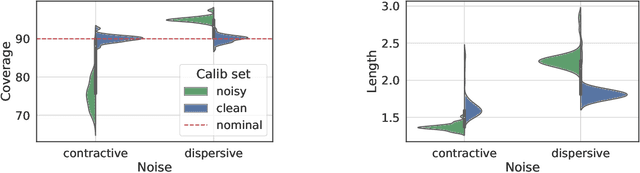
We study the robustness of conformal prediction, a powerful tool for uncertainty quantification, to label noise. Our analysis tackles both regression and classification problems, characterizing when and how it is possible to construct uncertainty sets that correctly cover the unobserved noiseless ground truth labels. Through stylized theoretical examples and practical experiments, we argue that naive conformal prediction covers the noiseless ground truth label unless the noise distribution is adversarially designed. This leads us to believe that correcting for label noise is unnecessary except for pathological data distributions or noise sources. In such cases, we can also correct for noise of bounded size in the conformal prediction algorithm in order to ensure correct coverage of the ground truth labels without score or data regularity.