Arshad Shaikh
Improved Representation Learning for Session-based Recommendation
Jul 04, 2021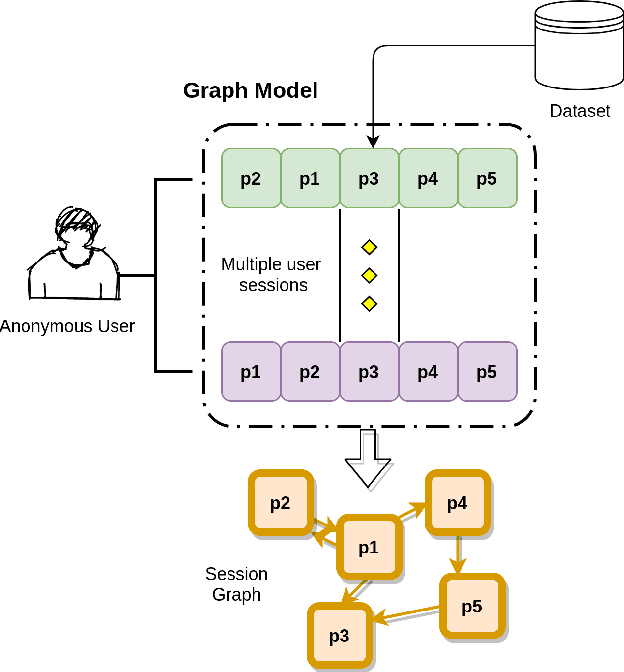

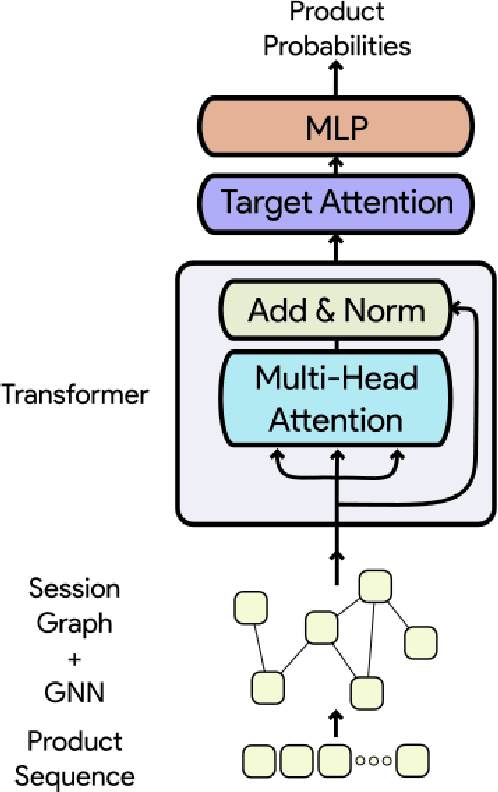
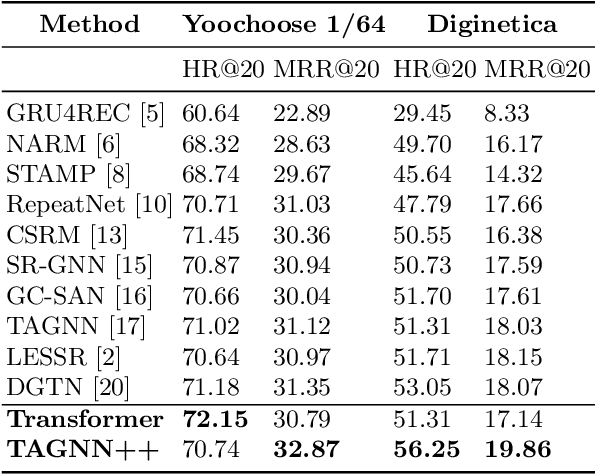
Abstract:Session-based recommendation systems suggest relevant items to users by modeling user behavior and preferences using short-term anonymous sessions. Existing methods leverage Graph Neural Networks (GNNs) that propagate and aggregate information from neighboring nodes i.e., local message passing. Such graph-based architectures have representational limits, as a single sub-graph is susceptible to overfit the sequential dependencies instead of accounting for complex transitions between items in different sessions. We propose using a Transformer in combination with a target attentive GNN, which allows richer Representation Learning. Our experimental results and ablation show that our proposed method outperforms the existing methods on real-world benchmark datasets.
On The Connection of Benford's Law and Neural Networks
Feb 05, 2021



Abstract:Benford's law, also called Significant Digit Law, is observed in many naturally occurring data-sets. For instance, the physical constants such as Gravitational, Coulomb's Constant, etc., follow this law. In this paper, we define a score, $MLH$, for how closely a Neural Network's Weights match Benford's law. We show that Neural Network Weights follow Benford's Law regardless of the initialization method. We make a striking connection between Generalization and the $MLH$ of the network. We provide evidence that several architectures from AlexNet to ResNeXt trained on ImageNet, Transformers (BERT, Electra, etc.), and other pre-trained models on a wide variety of tasks have a strong correlation between their test performance and the $MLH$. We also investigate the influence of Data in the Weights to explain why NNs possibly follow Benford's Law. With repeated experiments on multiple datasets using MLPs, CNNs, and LSTMs, we provide empirical evidence that there is a connection between $MLH$ while training, overfitting. Understanding this connection between Benford's Law and Neural Networks promises a better comprehension of the latter.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge