Social learning via actions in bandit environments

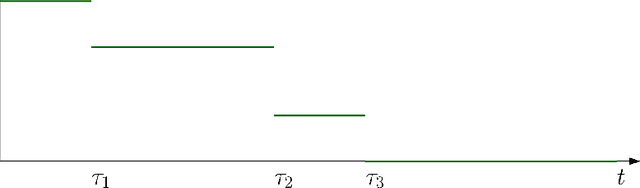
I study a game of strategic exploration with private payoffs and public actions in a Bayesian bandit setting. In particular, I look at cascade equilibria, in which agents switch over time from the risky action to the riskless action only when they become sufficiently pessimistic. I show that these equilibria exist under some conditions and establish their salient properties. Individual exploration in these equilibria can be more or less than the single-agent level depending on whether the agents start out with a common prior or not, but the most optimistic agent always underexplores. I also show that allowing the agents to write enforceable ex-ante contracts will lead to the most ex-ante optimistic agent to buy all payoff streams, providing an explanation to the buying out of smaller start-ups by more established firms.

Risk Aversion In Learning Algorithms and an Application To Recommendation Systems

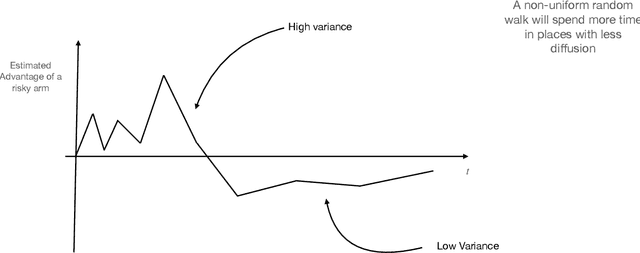
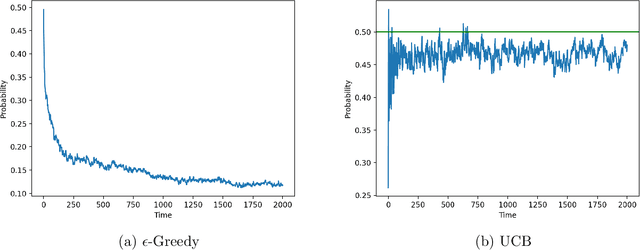
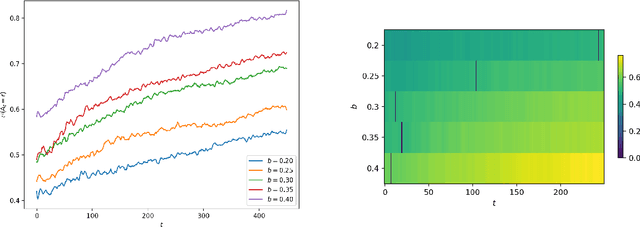
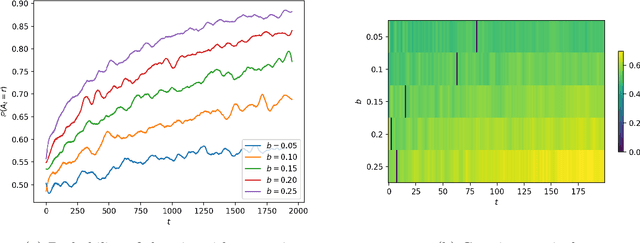
Consider a bandit learning environment. We demonstrate that popular learning algorithms such as Upper Confidence Band (UCB) and $\varepsilon$-Greedy exhibit risk aversion: when presented with two arms of the same expectation, but different variance, the algorithms tend to not choose the riskier, i.e. higher variance, arm. We prove that $\varepsilon$-Greedy chooses the risky arm with probability tending to $0$ when faced with a deterministic and a Rademacher-distributed arm. We show experimentally that UCB also shows risk-averse behavior, and that risk aversion is present persistently in early rounds of learning even if the riskier arm has a slightly higher expectation. We calibrate our model to a recommendation system and show that algorithmic risk aversion can decrease consumer surplus and increase homogeneity. We discuss several extensions to other bandit algorithms, reinforcement learning, and investigate the impacts of algorithmic risk aversion for decision theory.