Prognostic Covariate Adjustment for Logistic Regression in Randomized Controlled Trials

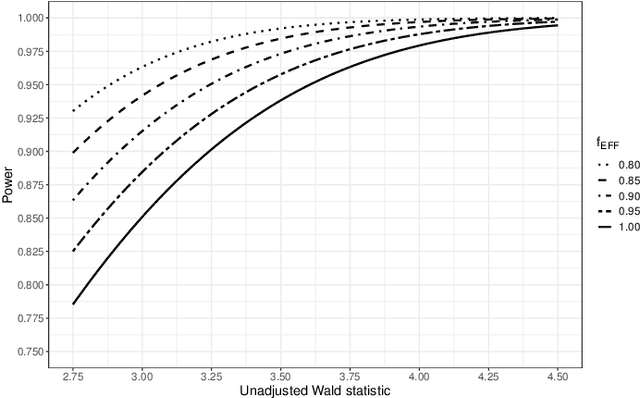
Randomized controlled trials (RCTs) with binary primary endpoints introduce novel challenges for inferring the causal effects of treatments. The most significant challenge is non-collapsibility, in which the conditional odds ratio estimand under covariate adjustment differs from the unconditional estimand in the logistic regression analysis of RCT data. This issue gives rise to apparent paradoxes, such as the variance of the estimator for the conditional odds ratio from a covariate-adjusted model being greater than the variance of the estimator from the unadjusted model. We address this challenge in the context of adjustment based on predictions of control outcomes from generative artificial intelligence (AI) algorithms, which are referred to as prognostic scores. We demonstrate that prognostic score adjustment in logistic regression increases the power of the Wald test for the conditional odds ratio under a fixed sample size, or alternatively reduces the necessary sample size to achieve a desired power, compared to the unadjusted analysis. We derive formulae for prospective calculations of the power gain and sample size reduction that can result from adjustment for the prognostic score. Furthermore, we utilize g-computation to expand the scope of prognostic score adjustment to inferences on the marginal risk difference, relative risk, and odds ratio estimands. We demonstrate the validity of our formulae via extensive simulation studies that encompass different types of logistic regression model specifications. Our simulation studies also indicate how prognostic score adjustment can reduce the variance of g-computation estimators for the marginal estimands while maintaining frequentist properties such as asymptotic unbiasedness and Type I error rate control. Our methodology can ultimately enable more definitive and conclusive analyses for RCTs with binary primary endpoints.

Bayesian Prognostic Covariate Adjustment With Additive Mixture Priors

Effective and rapid decision-making from randomized controlled trials (RCTs) requires unbiased and precise treatment effect inferences. Two strategies to address this requirement are to adjust for covariates that are highly correlated with the outcome, and to leverage historical control information via Bayes' theorem. We propose a new Bayesian prognostic covariate adjustment methodology, referred to as Bayesian PROCOVA, that combines these two strategies. Covariate adjustment is based on generative artificial intelligence (AI) algorithms that construct a digital twin generator (DTG) for RCT participants. The DTG is trained on historical control data and yields a digital twin (DT) probability distribution for each participant's control outcome. The expectation of the DT distribution defines the single covariate for adjustment. Historical control information are leveraged via an additive mixture prior with two components: an informative prior probability distribution specified based on historical control data, and a non-informative prior distribution. The weight parameter in the mixture has a prior distribution as well, so that the entire additive mixture prior distribution is completely pre-specifiable and does not involve any information from the RCT. We establish an efficient Gibbs algorithm for sampling from the posterior distribution, and derive closed-form expressions for the posterior mean and variance of the treatment effect conditional on the weight parameter, of Bayesian PROCOVA. We evaluate the bias control and variance reduction of Bayesian PROCOVA compared to frequentist prognostic covariate adjustment (PROCOVA) via simulation studies that encompass different types of discrepancies between the historical control and RCT data. Ultimately, Bayesian PROCOVA can yield informative treatment effect inferences with fewer control participants, accelerating effective decision-making.

A Weighted Prognostic Covariate Adjustment Method for Efficient and Powerful Treatment Effect Inferences in Randomized Controlled Trials

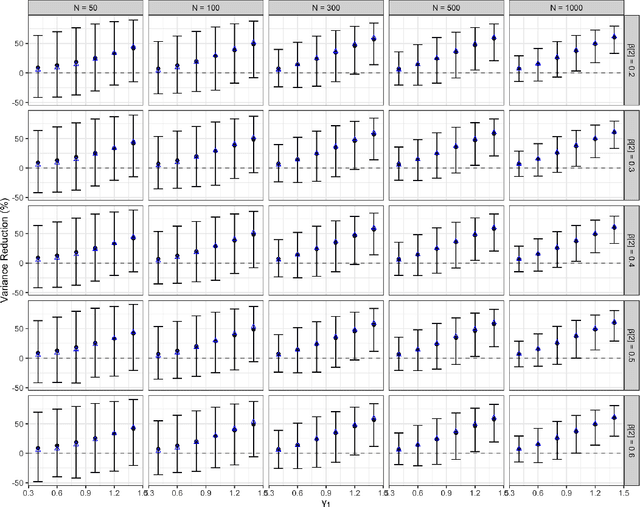
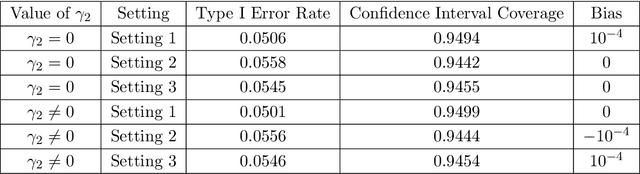
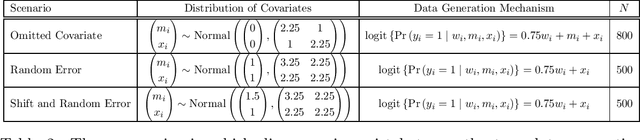
A crucial task for a randomized controlled trial (RCT) is to specify a statistical method that can yield an efficient estimator and powerful test for the treatment effect. A novel and effective strategy to obtain efficient and powerful treatment effect inferences is to incorporate predictions from generative artificial intelligence (AI) algorithms into covariate adjustment for the regression analysis of a RCT. Training a generative AI algorithm on historical control data enables one to construct a digital twin generator (DTG) for RCT participants, which utilizes a participant's baseline covariates to generate a probability distribution for their potential control outcome. Summaries of the probability distribution from the DTG are highly predictive of the trial outcome, and adjusting for these features via regression can thus improve the quality of treatment effect inferences, while satisfying regulatory guidelines on statistical analyses, for a RCT. However, a critical assumption in this strategy is homoskedasticity, or constant variance of the outcome conditional on the covariates. In the case of heteroskedasticity, existing covariate adjustment methods yield inefficient estimators and underpowered tests. We propose to address heteroskedasticity via a weighted prognostic covariate adjustment methodology (Weighted PROCOVA) that adjusts for both the mean and variance of the regression model using information obtained from the DTG. We prove that our method yields unbiased treatment effect estimators, and demonstrate via comprehensive simulation studies and case studies from Alzheimer's disease that it can reduce the variance of the treatment effect estimator, maintain the Type I error rate, and increase the power of the test for the treatment effect from 80% to 85%~90% when the variances from the DTG can explain 5%~10% of the variation in the RCT participants' outcomes.