Prognostic Covariate Adjustment for Logistic Regression in Randomized Controlled Trials
Paper and Code
Feb 29, 2024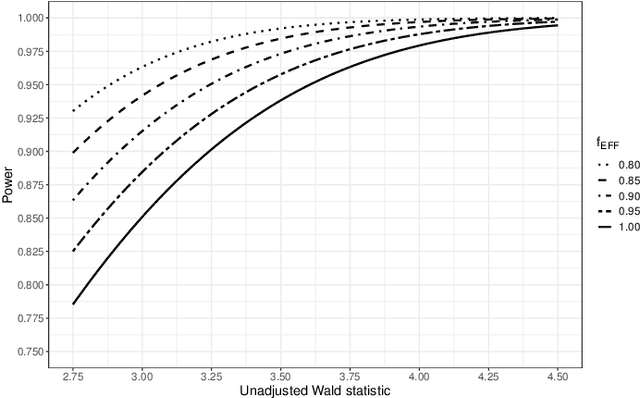

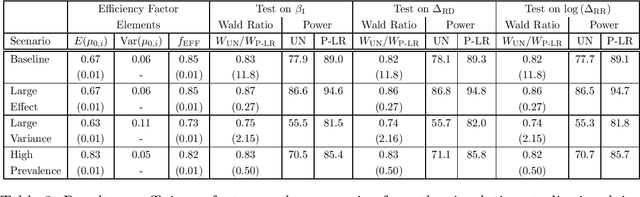
Randomized controlled trials (RCTs) with binary primary endpoints introduce novel challenges for inferring the causal effects of treatments. The most significant challenge is non-collapsibility, in which the conditional odds ratio estimand under covariate adjustment differs from the unconditional estimand in the logistic regression analysis of RCT data. This issue gives rise to apparent paradoxes, such as the variance of the estimator for the conditional odds ratio from a covariate-adjusted model being greater than the variance of the estimator from the unadjusted model. We address this challenge in the context of adjustment based on predictions of control outcomes from generative artificial intelligence (AI) algorithms, which are referred to as prognostic scores. We demonstrate that prognostic score adjustment in logistic regression increases the power of the Wald test for the conditional odds ratio under a fixed sample size, or alternatively reduces the necessary sample size to achieve a desired power, compared to the unadjusted analysis. We derive formulae for prospective calculations of the power gain and sample size reduction that can result from adjustment for the prognostic score. Furthermore, we utilize g-computation to expand the scope of prognostic score adjustment to inferences on the marginal risk difference, relative risk, and odds ratio estimands. We demonstrate the validity of our formulae via extensive simulation studies that encompass different types of logistic regression model specifications. Our simulation studies also indicate how prognostic score adjustment can reduce the variance of g-computation estimators for the marginal estimands while maintaining frequentist properties such as asymptotic unbiasedness and Type I error rate control. Our methodology can ultimately enable more definitive and conclusive analyses for RCTs with binary primary endpoints.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge