Bayesian Counterfactual Prediction Models for HIV Care Retention with Incomplete Outcome and Covariate Information

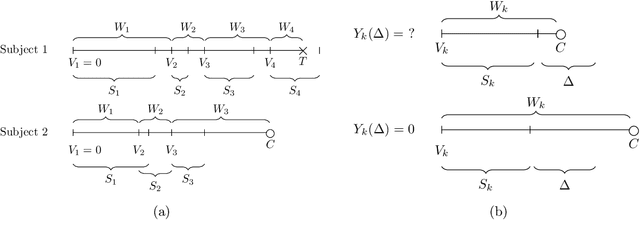
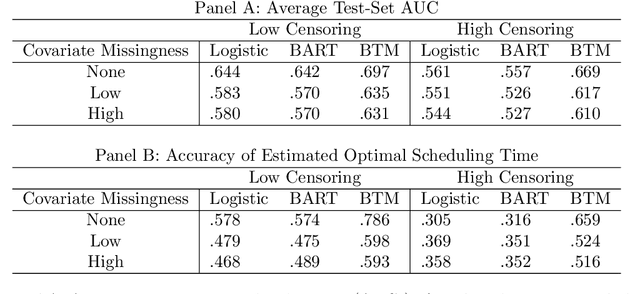
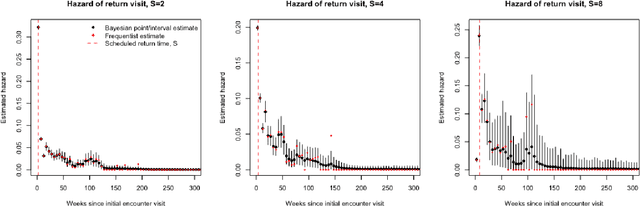
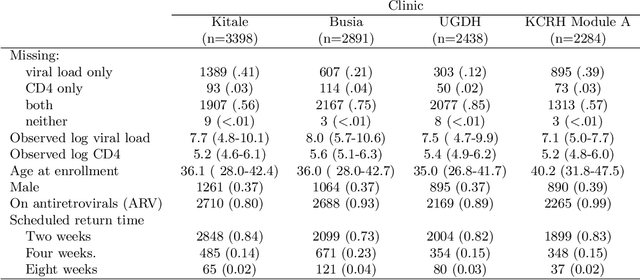
Like many chronic diseases, human immunodeficiency virus (HIV) is managed over time at regular clinic visits. At each visit, patient features are assessed, treatments are prescribed, and a subsequent visit is scheduled. There is a need for data-driven methods for both predicting retention and recommending scheduling decisions that optimize retention. Prediction models can be useful for estimating retention rates across a range of scheduling options. However, training such models with electronic health records (EHR) involves several complexities. First, formal causal inference methods are needed to adjust for observed confounding when estimating retention rates under counterfactual scheduling decisions. Second, competing events such as death preclude retention, while censoring events render retention missing. Third, inconsistent monitoring of features such as viral load and CD4 count lead to covariate missingness. This paper presents an all-in-one approach for both predicting HIV retention and optimizing scheduling while accounting for these complexities. We formulate and identify causal retention estimands in terms of potential return-time under a hypothetical scheduling decision. Flexible Bayesian approaches are used to model the observed return-time distribution while accounting for competing and censoring events and form posterior point and uncertainty estimates for these estimands. We address the urgent need for data-driven decision support in HIV care by applying our method to EHR from the Academic Model Providing Access to Healthcare (AMPATH) - a consortium of clinics that treat HIV in Western Kenya.

A Bayesian Framework for Causal Analysis of Recurrent Events in Presence of Immortal Risk

Observational studies of recurrent event rates are common in biomedical statistics. Broadly, the goal is to estimate differences in event rates under two treatments within a defined target population over a specified followup window. Estimation with observational claims data is challenging because while membership in the target population is defined in terms of eligibility criteria, treatment is rarely assigned exactly at the time of eligibility. Ad-hoc solutions to this timing misalignment, such as assigning treatment at eligibility based on subsequent assignment, incorrectly attribute prior event rates to treatment - resulting in immortal risk bias. Even if eligibility and treatment are aligned, a terminal event process (e.g. death) often stops the recurrent event process of interest. Both processes are also censored so that events are not observed over the entire followup window. Our approach addresses misalignment by casting it as a treatment switching problem: some patients are on treatment at eligibility while others are off treatment but may switch to treatment at a specified time - if they survive long enough. We define and identify an average causal effect of switching under specified causal assumptions. Estimation is done using a g-computation framework with a joint semiparametric Bayesian model for the death and recurrent event processes. Computing the estimand for various switching times allows us to assess the impact of treatment timing. We apply the method to contrast hospitalization rates under different opioid treatment strategies among patients with chronic back pain using Medicare claims data.

Bayesian Semiparametric Model for Sequential Treatment Decisions with Informative Timing

We develop a Bayesian semi-parametric model for the estimating the impact of dynamic treatment rules on survival among patients diagnosed with pediatric acute myeloid leukemia (AML). The data consist of a subset of patients enrolled in the phase III AAML1031 clinical trial in which patients move through a sequence of four treatment courses. At each course, they undergo treatment that may or may not include anthracyclines (ACT). While ACT is known to be effective at treating AML, it is also cardiotoxic and can lead to early death for some patients. Our task is to estimate the potential survival probability under hypothetical dynamic ACT treatment strategies, but there are several impediments. First, since ACT was not randomized in the trial, its effect on survival is confounded over time. Second, subjects initiate the next course depending on when they recover from the previous course, making timing potentially informative of subsequent treatment and survival. Third, patients may die or drop out before ever completing the full treatment sequence. We develop a generative Bayesian semi-parametric model based on Gamma Process priors to address these complexities. At each treatment course, the model captures subjects' transition to subsequent treatment or death in continuous time under a given rule. A g-computation procedure is used to compute a posterior over potential survival probability that is adjusted for time-varying confounding. Using this approach, we conduct posterior inference for the efficacy of hypothetical treatment rules that dynamically modify ACT based on evolving cardiac function.

A Practical Introduction to Bayesian Estimation of Causal Effects: Parametric and Nonparametric Approaches

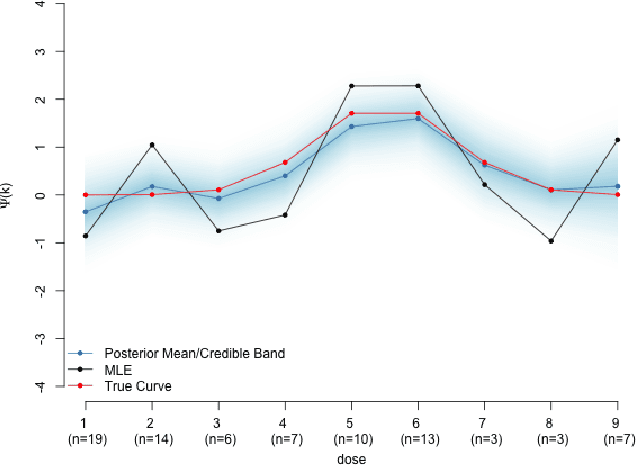
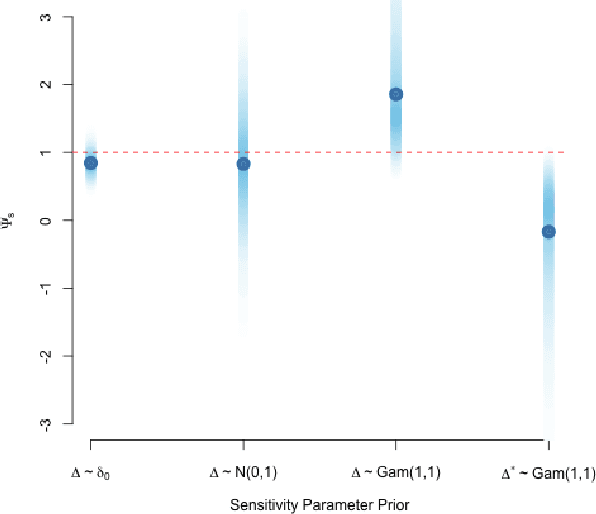
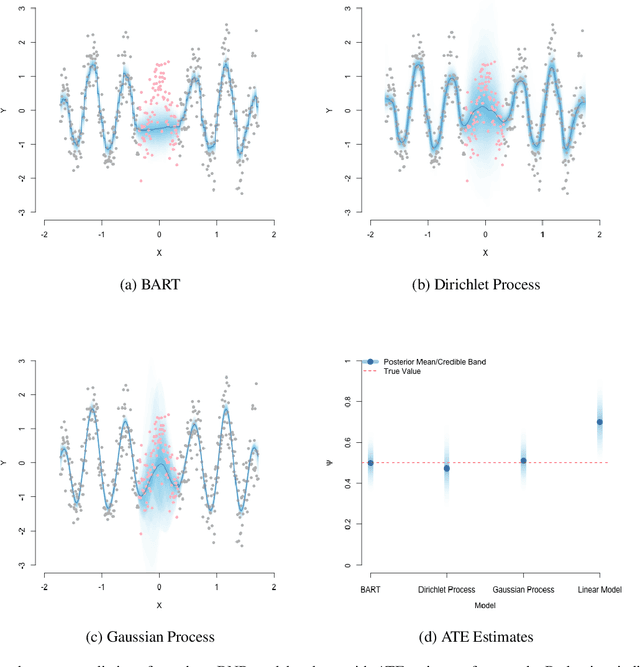
Substantial advances in Bayesian methods for causal inference have been developed in recent years. We provide an introduction to Bayesian inference for causal effects for practicing statisticians who have some familiarity with Bayesian models and would like an overview of what it can add to causal estimation in practical settings. In the paper, we demonstrate how priors can induce shrinkage and sparsity on parametric models and be used to perform probabilistic sensitivity analyses around causal assumptions. We provide an overview of nonparametric Bayesian estimation and survey their applications in the causal inference literature. Inference in the point-treatment and time-varying treatment settings are considered. For the latter, we explore both static and dynamic treatment regimes. Throughout, we illustrate implementation using off-the-shelf open source software. We hope the reader will walk away with implementation-level knowledge of Bayesian causal inference using both parametric and nonparametric models. All synthetic examples and code used in the paper are publicly available on a companion GitHub repository.

Bayesian Nonparametric Cost-Effectiveness Analyses: Causal Estimation and Adaptive Subgroup Discovery

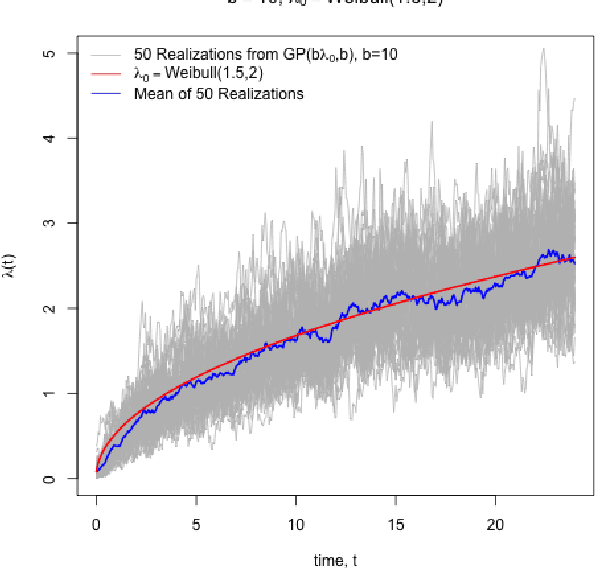
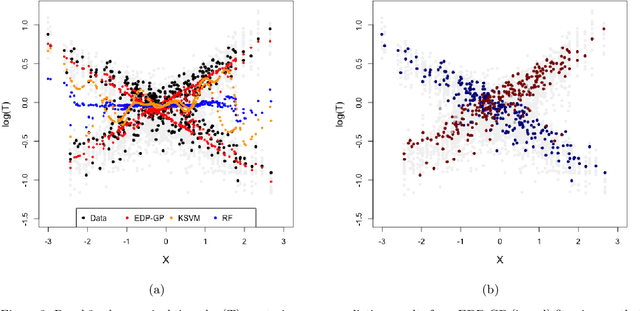
Cost-effectiveness analyses (CEAs) are at the center of health economic decision making. While these analyses help policy analysts and economists determine coverage, inform policy, and guide resource allocation, they are statistically challenging for several reasons. Cost and effectiveness are correlated and follow complex joint distributions which cannot be captured parametrically. Effectiveness (often measured as increased survival time) and cost both tend to be right-censored. Moreover, CEAs are often conducted using observational data with non-random treatment assignment. Policy-relevant causal estimation therefore requires robust confounding control. Finally, current CEA methods do not address cost-effectiveness heterogeneity in a principled way - opting to either present marginal results or cost-effectiveness results for pre-specified subgroups. Motivated by these challenges, we develop a nonparametric Bayesian model for joint cost-survival distributions in the presence of censoring. Our approach utilizes an Enriched Dirichlet Process prior on the covariate effects of cost and survival time, while using a separate Gamma Process prior on the baseline survival time hazard. Causal CEA estimands are identified and estimated via a Bayesian nonparametric g-computation procedure. Finally, we propose leveraging the induced clustering of the Enriched Dirichlet Process to adaptively discover subgroups of patients with different cost-effectiveness profiles. We outline an MCMC procedure for full posterior inference, evaluate frequentist properties via simulations, and apply our model to an observational study of endometrial cancer therapies using medical insurance claims data.