Bayesian Nonparametric Cost-Effectiveness Analyses: Causal Estimation and Adaptive Subgroup Discovery
Paper and Code
Feb 11, 2020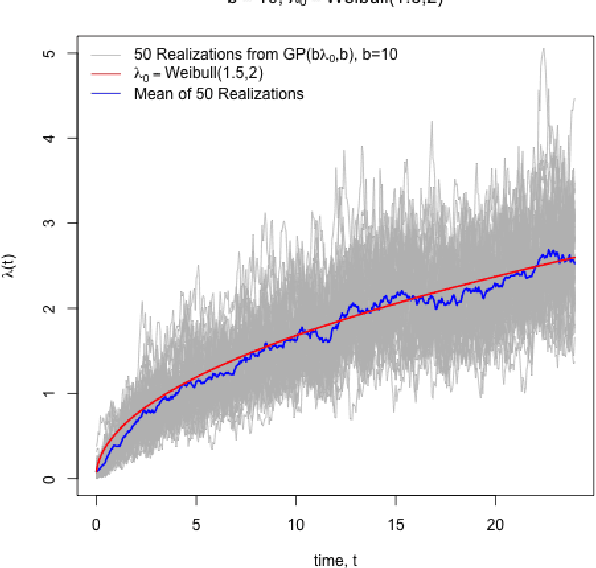

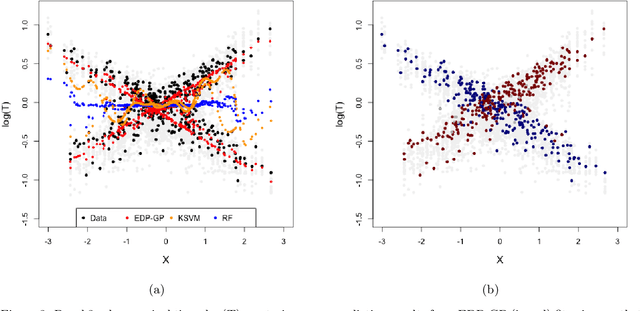
Cost-effectiveness analyses (CEAs) are at the center of health economic decision making. While these analyses help policy analysts and economists determine coverage, inform policy, and guide resource allocation, they are statistically challenging for several reasons. Cost and effectiveness are correlated and follow complex joint distributions which cannot be captured parametrically. Effectiveness (often measured as increased survival time) and cost both tend to be right-censored. Moreover, CEAs are often conducted using observational data with non-random treatment assignment. Policy-relevant causal estimation therefore requires robust confounding control. Finally, current CEA methods do not address cost-effectiveness heterogeneity in a principled way - opting to either present marginal results or cost-effectiveness results for pre-specified subgroups. Motivated by these challenges, we develop a nonparametric Bayesian model for joint cost-survival distributions in the presence of censoring. Our approach utilizes an Enriched Dirichlet Process prior on the covariate effects of cost and survival time, while using a separate Gamma Process prior on the baseline survival time hazard. Causal CEA estimands are identified and estimated via a Bayesian nonparametric g-computation procedure. Finally, we propose leveraging the induced clustering of the Enriched Dirichlet Process to adaptively discover subgroups of patients with different cost-effectiveness profiles. We outline an MCMC procedure for full posterior inference, evaluate frequentist properties via simulations, and apply our model to an observational study of endometrial cancer therapies using medical insurance claims data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge