Channel Training and Estimation for Reconfigurable Intelligent Surfaces: Exposition of Principles, Approaches, and Open Problems

Reconfigurable intelligent surfaces (RIS) are passive controllable arrays of small reflectors that direct electromagnetic energy towards or away from the target nodes, thereby allowing better management of signals and interference in a wireless network. The RIS has the potential for significantly improving the performance of wireless networks. Unfortunately, RIS also multiplies the number of Channel State Information (CSI) coefficients between the transmitter and receiver, which magnifies the challenges in estimating and communicating the channel state information. Furthermore, the simplicity and cost-effectiveness of the passive RIS also implies that the incoming links are not locally estimated at the RIS, and fresh pilots are not inserted into outgoing RIS links. This introduces new challenges for training and estimation of channel state information. The rapid growth of the literature on CSI acquisition in RIS-aided systems has been accompanied by variations in the underlying assumptions, models, and notation, which can obscure the similarities and differences of various techniques, and their relative merits. This paper presents a comprehensive exposition of principles and approaches in RIS channel estimation. The basic ideas underlying each class of techniques are reduced to their simplest form under a unified model and notation, and various approaches within each class are discussed. Several open problems in this area are identified and highlighted.

Community Detection with Known, Unknown, or Partially Known Auxiliary Latent Variables

Empirical observations suggest that in practice, community membership does not completely explain the dependency between the edges of an observation graph. The residual dependence of the graph edges are modeled in this paper, to first order, by auxiliary node latent variables that affect the statistics of the graph edges but carry no information about the communities of interest. We then study community detection in graphs obeying the stochastic block model and censored block model with auxiliary latent variables. We analyze the conditions for exact recovery when these auxiliary latent variables are unknown, representing unknown nuisance parameters or model mismatch. We also analyze exact recovery when these secondary latent variables have been either fully or partially revealed. Finally, we propose a semidefinite programming algorithm for recovering the desired labels when the secondary labels are either known or unknown. We show that exact recovery is possible by semidefinite programming down to the respective maximum likelihood exact recovery threshold.

Semidefinite Programming for Community Detection with Side Information

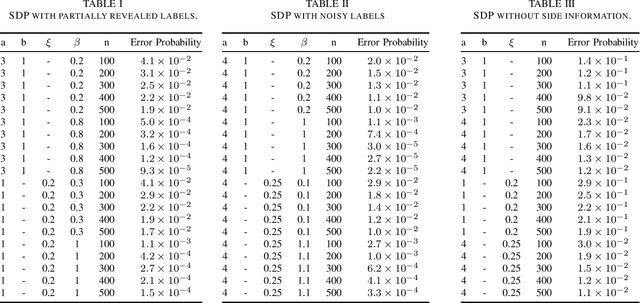
This paper produces an efficient Semidefinite Programming (SDP) solution for community detection that incorporates non-graph data, which in this context is known as side information. SDP is an efficient solution for standard community detection on graphs. We formulate a semi-definite relaxation for the maximum likelihood estimation of node labels, subject to observing both graph and non-graph data. This formulation is distinct from the SDP solution of standard community detection, but maintains its desirable properties. We calculate the exact recovery threshold for three types of non-graph information, which in this paper are called side information: partially revealed labels, noisy labels, as well as multiple observations (features) per node with arbitrary but finite cardinality. We find that SDP has the same exact recovery threshold in the presence of side information as maximum likelihood with side information. Thus, the methods developed herein are computationally efficient as well as asymptotically accurate for the solution of community detection in the presence of side information. Simulations show that the asymptotic results of this paper can also shed light on the performance of SDP for graphs of modest size.

Community Detection: Exact Recovery in Weighted Graphs

In community detection, the exact recovery of communities (clusters) has been mainly investigated under the general stochastic block model with edges drawn from Bernoulli distributions. This paper considers the exact recovery of communities in a complete graph in which the graph edges are drawn from either a set of Gaussian distributions with community-dependent means and variances, or a set of exponential distributions with community-dependent means. For each case, we introduce a new semi-metric that describes sufficient and necessary conditions of exact recovery. The necessary and sufficient conditions are asymptotically tight. The analysis is also extended to incomplete, fully connected weighted graphs.

New GCNN-Based Architecture for Semi-Supervised Node Classification

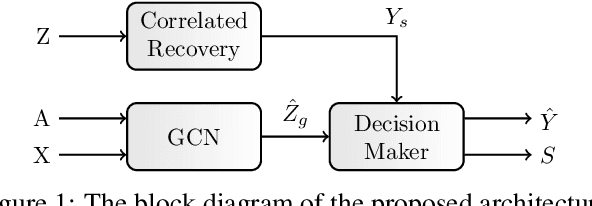
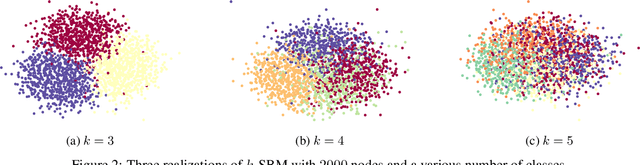
The nodes of a graph existing in a specific cluster are more likely to connect to each other than with other nodes in the graph. Then revealing some information about the nodes, the structure of the graph (the graph edges) provides this opportunity to know more information about the other nodes. From this perspective, this paper revisits the node classification task in a semi-supervised scenario by graph convolutional neural network. The goal is to benefit from the flow of information that circulates around the revealed node labels. For this aim, this paper provides a new graph convolutional neural network architecture. This architecture benefits efficiently from the revealed training nodes, the node features, and the graph structure. On the other hand, in many applications, non-graph observations (side information) exist beside a given graph realization. The non-graph observations are usually independent of the graph structure. This paper shows that the proposed architecture is also powerful in combining a graph realization and independent non-graph observations. For both cases, the experiments on the synthetic and real-world datasets demonstrate that our proposed architecture achieves a higher prediction accuracy in comparison to the existing state-of-the-art methods for the node classification task.

Recovering a Single Community with Side Information

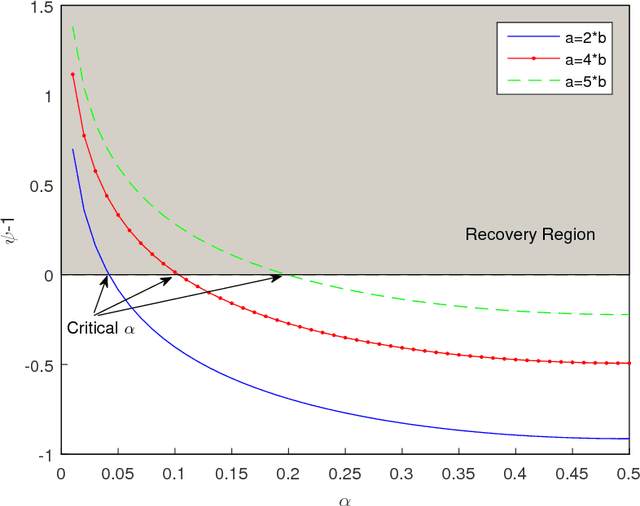
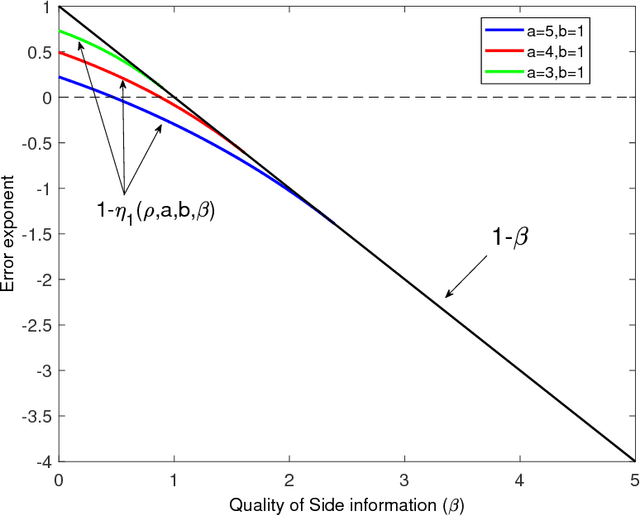
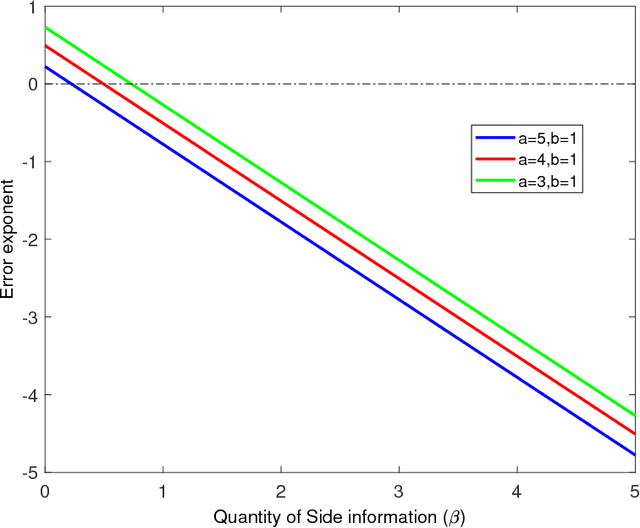
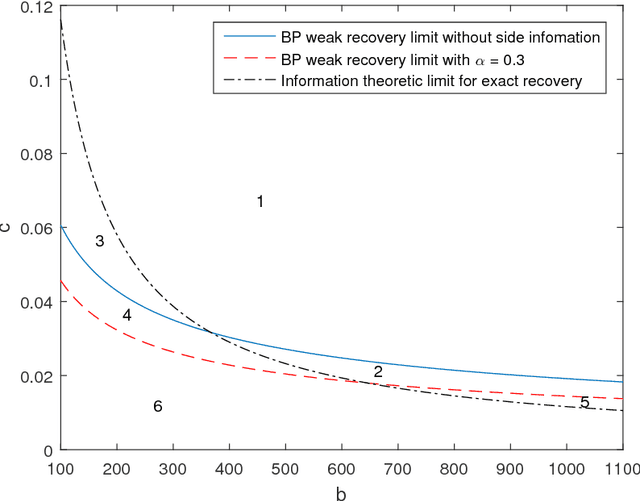
We study the effect of the quality and quantity of side information on the recovery of a hidden community of size $K=o(n)$ in a graph of size $n$. Side information for each node in the graph is modeled by a random vector with the following features: either the dimension of the vector is allowed to vary with $n$, while log-likelihood ratio (LLR) of each component with respect to the node label is fixed, or the LLR is allowed to vary and the vector dimension is fixed. These two models represent the variation in quality and quantity of side information. Under maximum likelihood detection, we calculate tight necessary and sufficient conditions for exact recovery of the labels. We demonstrate how side information needs to evolve with $n$ in terms of either its quantity, or quality, to improve the exact recovery threshold. A similar set of results are obtained for weak recovery. Under belief propagation, tight necessary and sufficient conditions for weak recovery are calculated when the LLRs are constant, and sufficient conditions when the LLRs vary with $n$. Moreover, we design and analyze a local voting procedure using side information that can achieve exact recovery when applied after belief propagation. The results for belief propagation are validated via simulations on finite synthetic data-sets, showing that the asymptotic results of this paper can also shed light on the performance at finite $n$.