Recovering a Single Community with Side Information
Paper and Code
Sep 05, 2018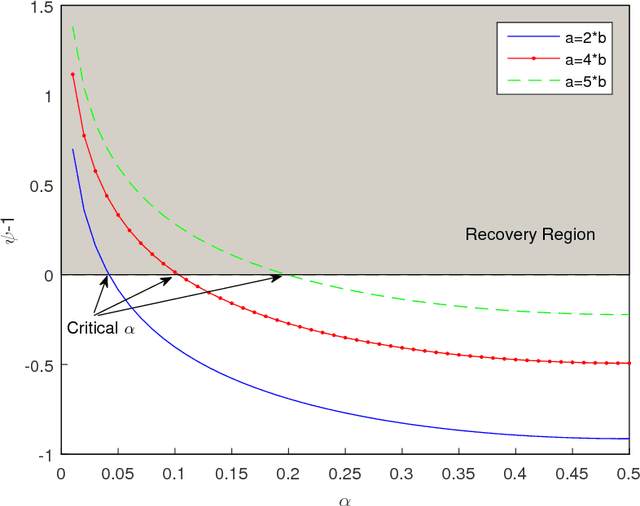
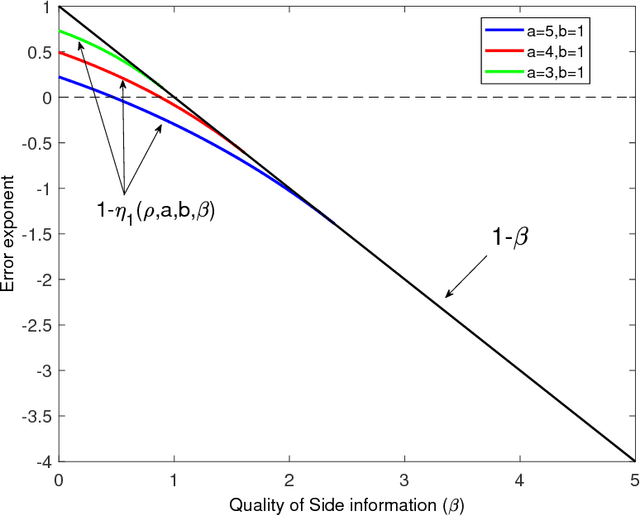
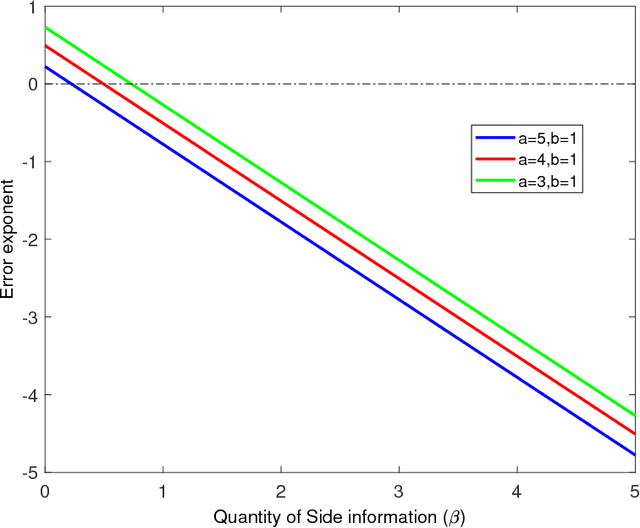
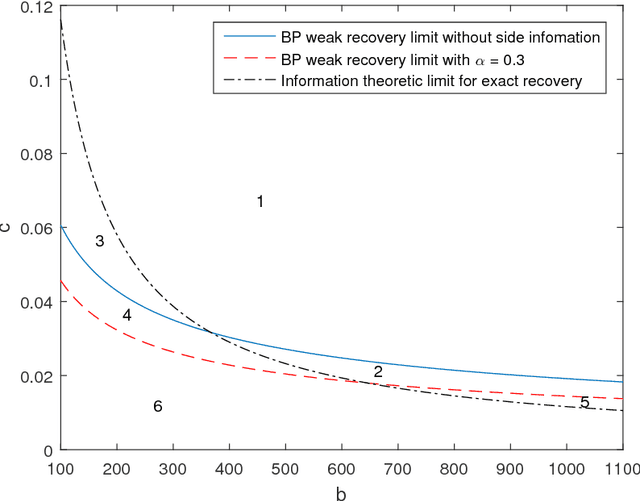
We study the effect of the quality and quantity of side information on the recovery of a hidden community of size $K=o(n)$ in a graph of size $n$. Side information for each node in the graph is modeled by a random vector with the following features: either the dimension of the vector is allowed to vary with $n$, while log-likelihood ratio (LLR) of each component with respect to the node label is fixed, or the LLR is allowed to vary and the vector dimension is fixed. These two models represent the variation in quality and quantity of side information. Under maximum likelihood detection, we calculate tight necessary and sufficient conditions for exact recovery of the labels. We demonstrate how side information needs to evolve with $n$ in terms of either its quantity, or quality, to improve the exact recovery threshold. A similar set of results are obtained for weak recovery. Under belief propagation, tight necessary and sufficient conditions for weak recovery are calculated when the LLRs are constant, and sufficient conditions when the LLRs vary with $n$. Moreover, we design and analyze a local voting procedure using side information that can achieve exact recovery when applied after belief propagation. The results for belief propagation are validated via simulations on finite synthetic data-sets, showing that the asymptotic results of this paper can also shed light on the performance at finite $n$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge