Graph Mining under Data scarcity

Multitude of deep learning models have been proposed for node classification in graphs. However, they tend to perform poorly under labeled-data scarcity. Although Few-shot learning for graphs has been introduced to overcome this problem, the existing models are not easily adaptable for generic graph learning frameworks like Graph Neural Networks (GNNs). Our work proposes an Uncertainty Estimator framework that can be applied on top of any generic GNN backbone network (which are typically designed for supervised/semi-supervised node classification) to improve the node classification performance. A neural network is used to model the Uncertainty Estimator as a probability distribution rather than probabilistic discrete scalar values. We train these models under the classic episodic learning paradigm in the $n$-way, $k$-shot fashion, in an end-to-end setting. Our work demonstrates that implementation of the uncertainty estimator on a GNN backbone network improves the classification accuracy under Few-shot setting without any meta-learning specific architecture. We conduct experiments on multiple datasets under different Few-shot settings and different GNN-based backbone networks. Our method outperforms the baselines, which demonstrates the efficacy of the Uncertainty Estimator for Few-shot node classification on graphs with a GNN.

Reinforced Continual Learning for Graphs

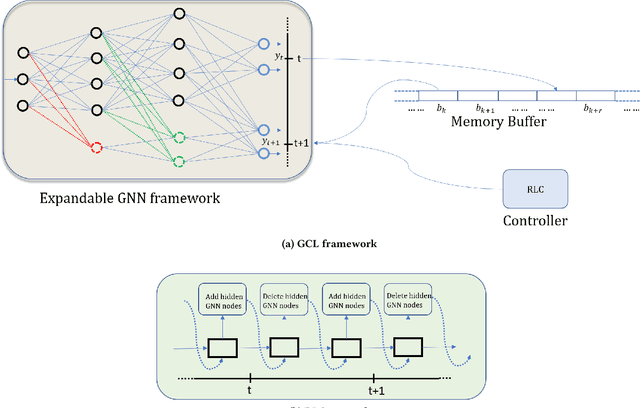
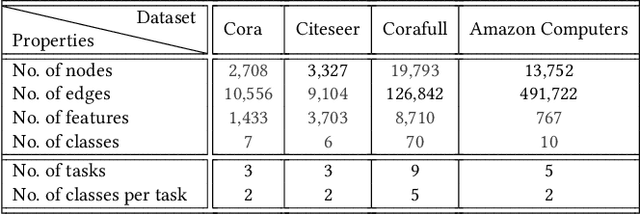
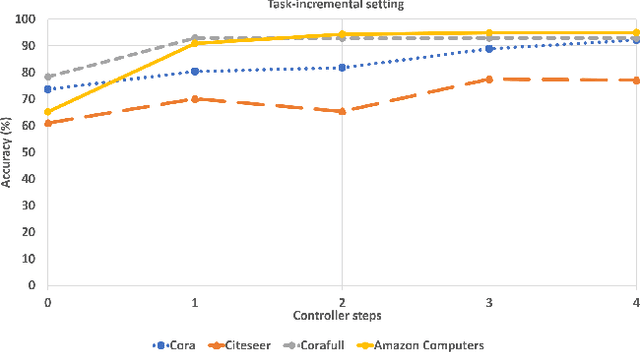
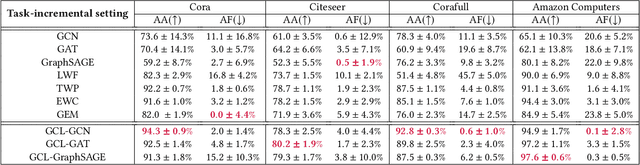
Graph Neural Networks (GNNs) have become the backbone for a myriad of tasks pertaining to graphs and similar topological data structures. While many works have been established in domains related to node and graph classification/regression tasks, they mostly deal with a single task. Continual learning on graphs is largely unexplored and existing graph continual learning approaches are limited to the task-incremental learning scenarios. This paper proposes a graph continual learning strategy that combines the architecture-based and memory-based approaches. The structural learning strategy is driven by reinforcement learning, where a controller network is trained in such a way to determine an optimal number of nodes to be added/pruned from the base network when new tasks are observed, thus assuring sufficient network capacities. The parameter learning strategy is underpinned by the concept of Dark Experience replay method to cope with the catastrophic forgetting problem. Our approach is numerically validated with several graph continual learning benchmark problems in both task-incremental learning and class-incremental learning settings. Compared to recently published works, our approach demonstrates improved performance in both the settings. The implementation code can be found at \url{https://github.com/codexhammer/gcl}.

Unsupervised Learning for Identifying High Eigenvector Centrality Nodes: A Graph Neural Network Approach

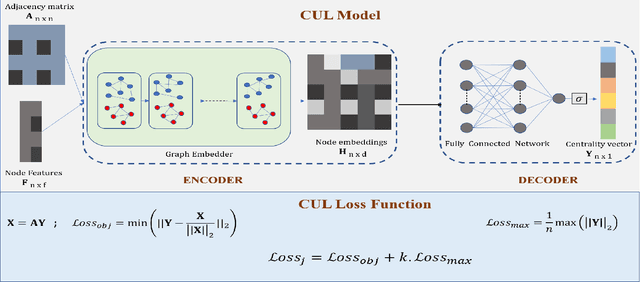
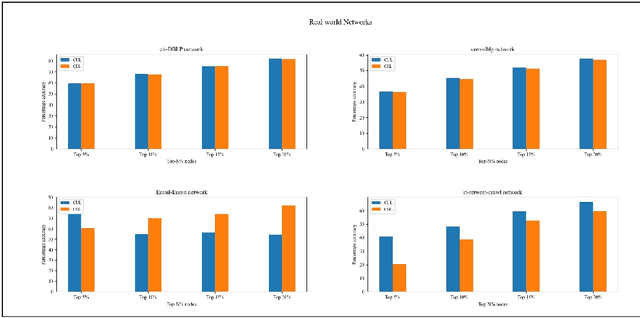
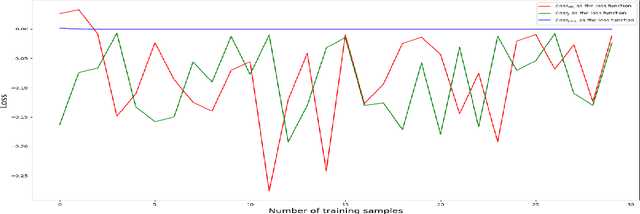
The existing methods to calculate the Eigenvector Centrality(EC) tend to not be robust enough for determination of EC in low time complexity or not well-scalable for large networks, hence rendering them practically unreliable/ computationally expensive. So, it is of the essence to develop a method that is scalable in low computational time. Hence, we propose a deep learning model for the identification of nodes with high Eigenvector Centrality. There have been a few previous works in identifying the high ranked nodes with supervised learning methods, but in real-world cases, the graphs are not labelled and hence deployment of supervised learning methods becomes a hazard and its usage becomes impractical. So, we devise CUL(Centrality with Unsupervised Learning) method to learn the relative EC scores in a network in an unsupervised manner. To achieve this, we develop an Encoder-Decoder based framework that maps the nodes to their respective estimated EC scores. Extensive experiments were conducted on different synthetic and real-world networks. We compared CUL against a baseline supervised method for EC estimation similar to some of the past works. It was observed that even with training on a minuscule number of training datasets, CUL delivers a relatively better accuracy score when identifying the higher ranked nodes than its supervised counterpart. We also show that CUL is much faster and has a smaller runtime than the conventional baseline method for EC computation. The code is available at https://github.com/codexhammer/CUL.