UDE-III: An Enhanced Unified Differential Evolution Algorithm for Constrained Optimization Problems

In this paper, an enhanced unified differential evolution algorithm, named UDE-III, is presented for real parameter-constrained optimization problems (COPs). The proposed UDE-III is a significantly enhanced version of the Improved UDE (i.e., IUDE or UDE-II), which secured the 1st rank in the CEC 2018 competition on real parameter COPs. To design UDE-III, we extensively targeted the weaknesses of UDE-II. Specifically, UDE-III uses three trial vector generation strategies - DE/rand/1, DE/current-to-rand/1, and DE/current-to-pbest/1. It is based on a dual population approach, and for each generation, it divides the current population into two sub-populations. In the top sub-population, it employs all three trial vector generation strategies on each target vector. On the other hand, the bottom sub-population employs strategy adaptation and one trial vector generation strategy is implemented on each target vector. The mutation operation in UDE-III is based on ranking-based mutation. Further, it employs the parameter adaptation principle of SHADE. The constraint handling principle in UDE-III is based on a combination of the feasibility rule and epsilon-constraint handling technique. We observed that stagnation is a major weakness of UDE-II. To overcome this weakness, we took inspiration from the best-discarded vector selection (BDVS) strategy proposed in the literature and integrated a novel strategy in UDE-III to address stagnation. Additionally, unlike UDE-II, UDE-III considers the size of the two sub-populations to be a design element. Moreover, in comparison to UDE-II, UDE-III improves upon the strategy adaptation, ranking-based mutation, and the constraint handling technique. The proposed UDE-III algorithm is tested on the 28 benchmark 30D problems provided for the CEC 2024 competition on real parameter COPs. The experimental results demonstrate the superiority of UDE-III over UDE-II.

A Multi-operator Ensemble LSHADE with Restart and Local Search Mechanisms for Single-objective Optimization

In recent years, multi-operator and multi-method algorithms have succeeded, encouraging their combination within single frameworks. Despite promising results, there remains room for improvement as only some evolutionary algorithms (EAs) consistently excel across all optimization problems. This paper proposes mLSHADE-RL, an enhanced version of LSHADE-cnEpSin, which is one of the winners of the CEC 2017 competition in real-parameter single-objective optimization. mLSHADE-RL integrates multiple EAs and search operators to improve performance further. Three mutation strategies such as DE/current-to-pbest-weight/1 with archive, DE/current-to-pbest/1 without archive, and DE/current-to-ordpbest-weight/1 are integrated in the original LSHADE-cnEpSin. A restart mechanism is also proposed to overcome the local optima tendency. Additionally, a local search method is applied in the later phase of the evolutionary procedure to enhance the exploitation capability of mLSHADE-RL. mLSHADE-RL is tested on 30 dimensions in the CEC 2024 competition on single objective bound constrained optimization, demonstrating superior performance over other state-of-the-art algorithms in producing high-quality solutions across various optimization scenarios.

Enhanced Multiobjective Evolutionary Algorithm based on Decomposition for Solving the Unit Commitment Problem

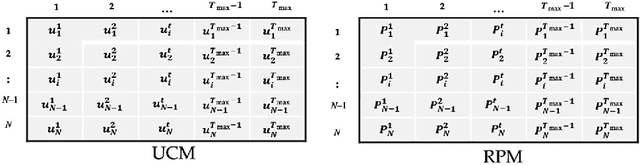
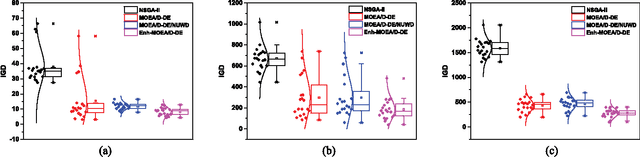
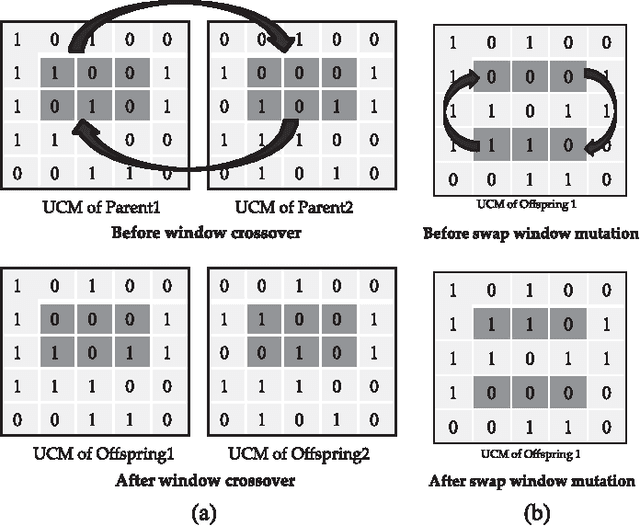
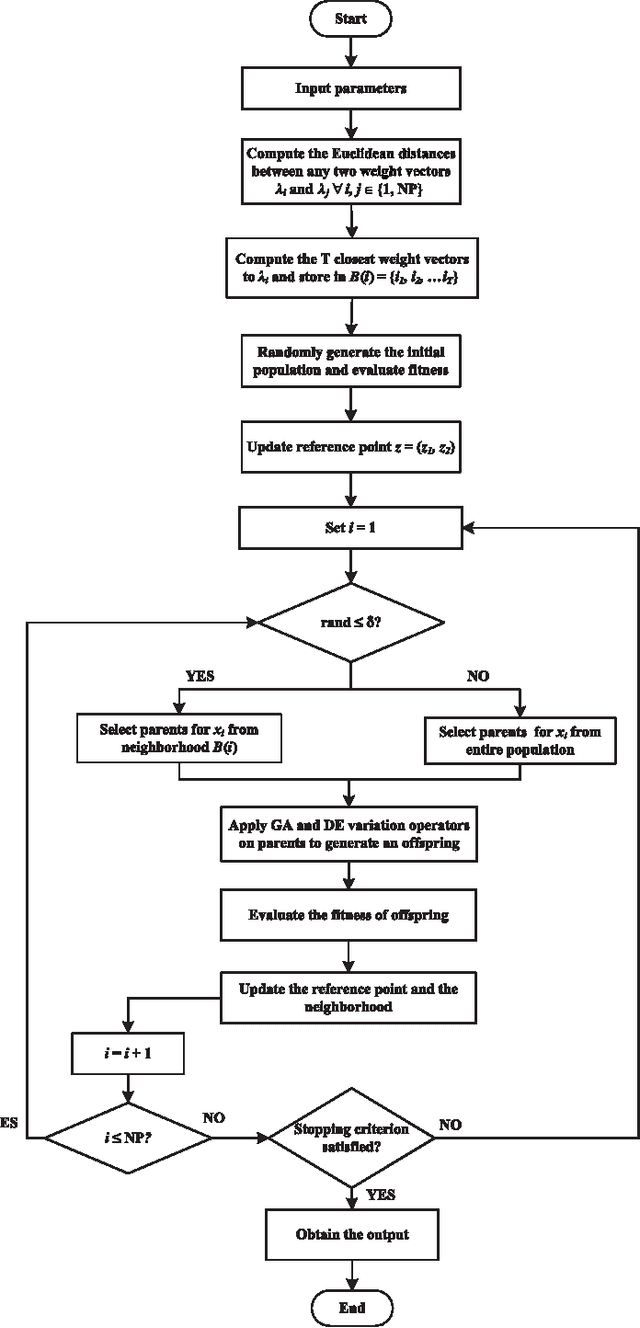
The unit commitment (UC) problem is a nonlinear, high-dimensional, highly constrained, mixed-integer power system optimization problem and is generally solved in the literature considering minimizing the system operation cost as the only objective. However, due to increasing environmental concerns, the recent attention has shifted to incorporating emission in the problem formulation. In this paper, a multi-objective evolutionary algorithm based on decomposition (MOEA/D) is proposed to solve the UC problem as a multi-objective optimization problem considering minimizing cost and emission as the multiple objec- tives. Since, UC problem is a mixed-integer optimization problem consisting of binary UC variables and continuous power dispatch variables, a novel hybridization strategy is proposed within the framework of MOEA/D such that genetic algorithm (GA) evolves the binary variables while differential evolution (DE) evolves the continuous variables. Further, a novel non-uniform weight vector distribution strategy is proposed and a parallel island model based on combination of MOEA/D with uniform and non-uniform weight vector distribution strategy is implemented to enhance the performance of the presented algorithm. Extensive case studies are presented on different test systems and the effectiveness of the proposed hybridization strategy, the non-uniform weight vector distribution strategy and parallel island model is verified through stringent simulated results. Further, exhaustive benchmarking against the algorithms proposed in the literature is presented to demonstrate the superiority of the proposed algorithm in obtaining significantly better converged and uniformly distributed trade-off solutions.