A Logical Characterization of the Preferred Models of Logic Programs with Ordered Disjunction

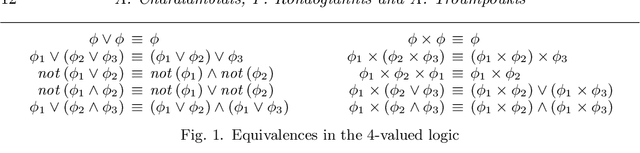
Logic Programs with Ordered Disjunction (LPODs) extend classical logic programs with the capability of expressing alternatives with decreasing degrees of preference in the heads of program rules. Despite the fact that the operational meaning of ordered disjunction is clear, there exists an important open issue regarding its semantics. In particular, there does not exist a purely model-theoretic approach for determining the most preferred models of an LPOD. At present, the selection of the most preferred models is performed using a technique that is not based exclusively on the models of the program and in certain cases produces counterintuitive results. We provide a novel, model-theoretic semantics for LPODs, which uses an additional truth value in order to identify the most preferred models of a program. We demonstrate that the proposed approach overcomes the shortcomings of the traditional semantics of LPODs. Moreover, the new approach can be used to define the semantics of a natural class of logic programs that can have both ordered and classical disjunctions in the heads of clauses. This allows programs that can express not only strict levels of preferences but also alternatives that are equally preferred. This work is under consideration for acceptance in TPLP.

Lexicographic Logic: a Many-valued Logic for Preference Representation

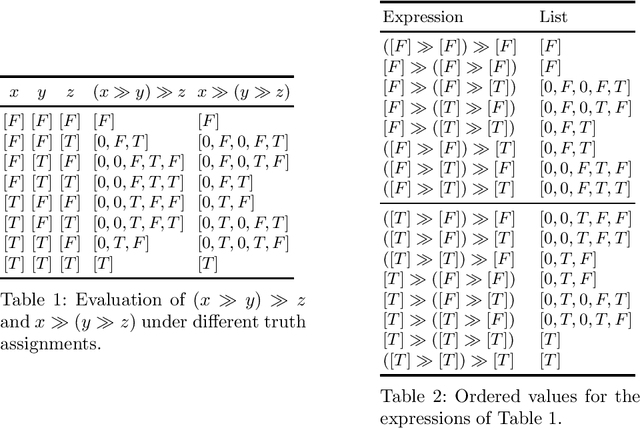
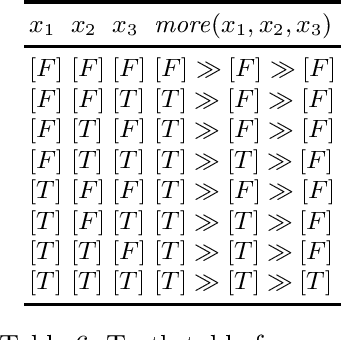
Logical formalisms provide a natural and concise means for specifying and reasoning about preferences. In this paper, we propose lexicographic logic, an extension of classical propositional logic that can express a variety of preferences, most notably lexicographic ones. The proposed logic supports a simple new connective whose semantics can be defined in terms of finite lists of truth values. We demonstrate that, despite the well-known theoretical limitations that pose barriers to the quantitative representation of lexicographic preferences, there exists a subset of the rational numbers over which the proposed new connective can be naturally defined. Lexicographic logic can be used to define in a simple way some well-known preferential operators, like "$A$ and if possible $B$", and "$A$ or failing that $B$". Moreover, many other hierarchical preferential operators can be defined using a systematic approach. We argue that the new logic is an effective formalism for ranking query results according to the satisfaction level of user preferences.