Lexicographic Logic: a Many-valued Logic for Preference Representation
Paper and Code
Dec 20, 2020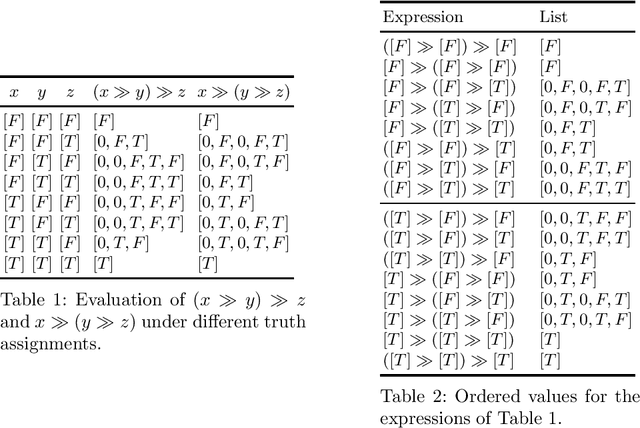


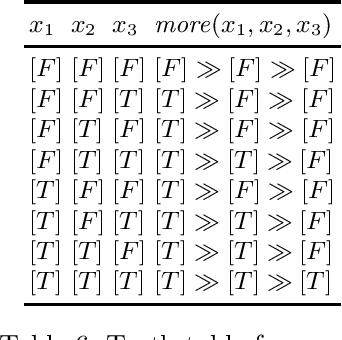
Logical formalisms provide a natural and concise means for specifying and reasoning about preferences. In this paper, we propose lexicographic logic, an extension of classical propositional logic that can express a variety of preferences, most notably lexicographic ones. The proposed logic supports a simple new connective whose semantics can be defined in terms of finite lists of truth values. We demonstrate that, despite the well-known theoretical limitations that pose barriers to the quantitative representation of lexicographic preferences, there exists a subset of the rational numbers over which the proposed new connective can be naturally defined. Lexicographic logic can be used to define in a simple way some well-known preferential operators, like "$A$ and if possible $B$", and "$A$ or failing that $B$". Moreover, many other hierarchical preferential operators can be defined using a systematic approach. We argue that the new logic is an effective formalism for ranking query results according to the satisfaction level of user preferences.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge