Fully distributed and resilient source seeking for robot swarms

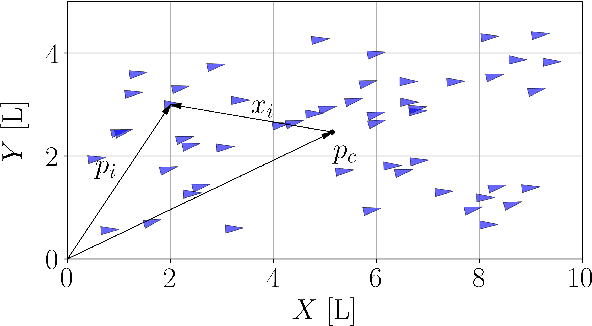
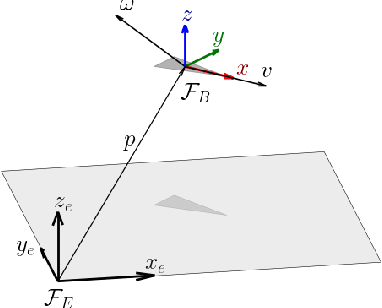
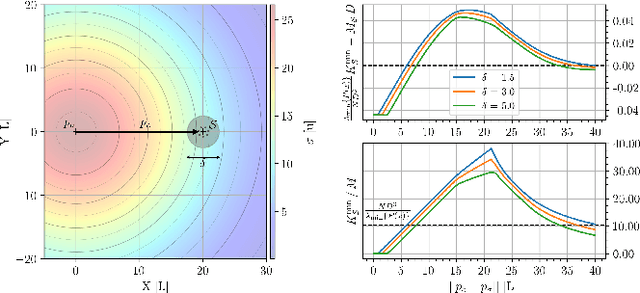
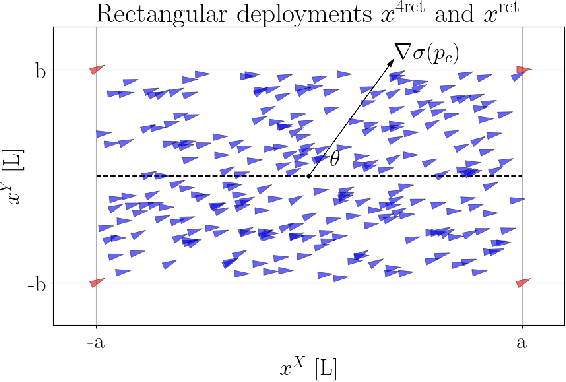
We propose a self-contained, resilient and fully distributed solution for locating the maximum of an unknown 3D scalar field using a swarm of robots that travel at constant speeds. Unlike conventional reactive methods relying on gradient information, our methodology enables the swarm to determine an ascending direction so that it approaches the source with arbitrary precision. Our source-seeking solution consists of three algorithms. The first two algorithms run sequentially and distributively at a high frequency providing barycentric coordinates and the ascending direction respectively to the individual robots. The third algorithm is the individual control law for a robot to track the estimated ascending direction. We show that the two algorithms with higher frequency have an exponential convergence to their eventual values since they are based on the standard consensus protocol for first-order dynamical systems; their high frequency depends on how fast the robots travel through the scalar field. The robots are not constrained to any particular geometric formation, and we study both discrete and continuous distributions of robots within swarm shapes. The shape analysis reveals the resiliency of our approach as expected in robot swarms, i.e., by amassing robots we ensure the source-seeking functionality in the event of missing or misplaced individuals or even if the robot network splits into two or more disconnected subnetworks. In addition, we also enhance the robustness of the algorithm by presenting conditions for \emph{optimal} swarm shapes, in the sense that the ascending directions can be closely parallel to the field's gradient. We exploit such an analysis so that the swarm can adapt to unknown environments by morphing its shape and maneuvering while still following an ascending direction.

Source-Seeking Problem with Robot Swarms

We present an algorithm to solve the problem of locating the source, or maxima, of a scalar field using a robot swarm. We demonstrate how the robot swarm determines its direction of movement to approach the source using only field intensity measurements taken by each robot. In contrast with the current literature, our algorithm accommodates a generic (non-degenerate) geometry for the swarm's formation. Additionally, we rigorously show the effectiveness of the algorithm even when the dynamics of the robots are complex, such as a unicycle with constant speed. Not requiring a strict geometry for the swarm significantly enhances its resilience. For example, this allows the swarm to change its size and formation in the presence of obstacles or other real-world factors, including the loss or addition of individuals to the swarm on the fly. For clarity, the article begins by presenting the algorithm for robots with free dynamics. In the second part, we demonstrate the algorithm's effectiveness even considering non-holonomic dynamics for the robots, using the vector field guidance paradigm. Finally, we verify and validate our algorithm with various numerical simulations.

Resilient source seeking with robot swarms

We present a solution for locating the source, or maximum, of an unknown scalar field using a swarm of mobile robots. Unlike relying on the traditional gradient information, the swarm determines an ascending direction to approach the source with arbitrary precision. The ascending direction is calculated from measurements of the field strength at the robot locations and their relative positions concerning the centroid. Rather than focusing on individual robots, we focus the analysis on the density of robots per unit area to guarantee a more resilient swarm, i.e., the functionality remains even if individuals go missing or are misplaced during the mission. We reinforce the robustness of the algorithm by providing sufficient conditions for the swarm shape so that the ascending direction is almost parallel to the gradient. The swarm can respond to an unexpected environment by morphing its shape and exploiting the existence of multiple ascending directions. Finally, we validate our approach numerically with hundreds of robots. The fact that a large number of robots always calculate an ascending direction compensates for the loss of individuals and mitigates issues arising from the actuator and sensor noises.