Singularity-Free Guiding Vector Field over Bézier's Curves Applied to Rovers Path Planning and Path Following

This paper presents a guidance algorithm for solving the problem of following parametric paths, as well as a curvature-varying speed setpoint for land-based car-type wheeled mobile robots (WMRs). The guidance algorithm relies on Singularity-Free Guiding Vector Fields SF-GVF. This novel GVF approach expands the desired robot path and the Guiding vector field to a higher dimensional space, in which an angular control function can be found to ensure global asymptotic convergence to the desired parametric path while avoiding field singularities. In SF-GVF, paths should follow a parametric definition. This feature makes using Bezier's curves attractive to define the robot's desired patch. The curvature-varying speed setpoint, combined with the guidance algorithm, eases the convergence to the path when physical restrictions exist, such as minimal turning radius or maximal lateral acceleration. We provide theoretical results, simulations, and outdoor experiments using a WMR platform assembled with off-the-shelf components.

Fully distributed and resilient source seeking for robot swarms

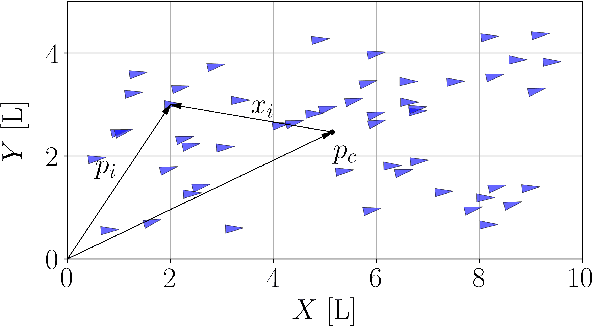
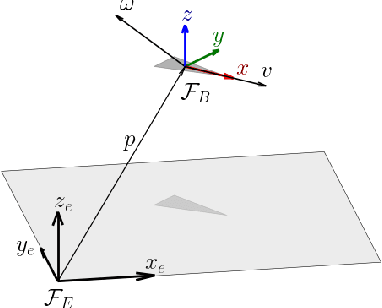
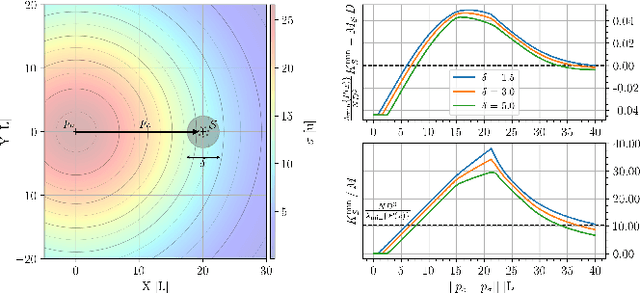
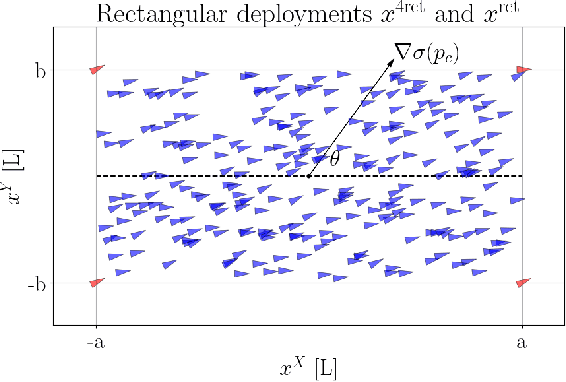
We propose a self-contained, resilient and fully distributed solution for locating the maximum of an unknown 3D scalar field using a swarm of robots that travel at constant speeds. Unlike conventional reactive methods relying on gradient information, our methodology enables the swarm to determine an ascending direction so that it approaches the source with arbitrary precision. Our source-seeking solution consists of three algorithms. The first two algorithms run sequentially and distributively at a high frequency providing barycentric coordinates and the ascending direction respectively to the individual robots. The third algorithm is the individual control law for a robot to track the estimated ascending direction. We show that the two algorithms with higher frequency have an exponential convergence to their eventual values since they are based on the standard consensus protocol for first-order dynamical systems; their high frequency depends on how fast the robots travel through the scalar field. The robots are not constrained to any particular geometric formation, and we study both discrete and continuous distributions of robots within swarm shapes. The shape analysis reveals the resiliency of our approach as expected in robot swarms, i.e., by amassing robots we ensure the source-seeking functionality in the event of missing or misplaced individuals or even if the robot network splits into two or more disconnected subnetworks. In addition, we also enhance the robustness of the algorithm by presenting conditions for \emph{optimal} swarm shapes, in the sense that the ascending directions can be closely parallel to the field's gradient. We exploit such an analysis so that the swarm can adapt to unknown environments by morphing its shape and maneuvering while still following an ascending direction.