Learning Bayesian Networks that enable full propagation of evidence

This paper builds on recent developments in Bayesian network (BN) structure learning under the controversial assumption that the input variables are dependent. This assumption is geared towards real-world datasets that incorporate variables which are assumed to be dependent. It aims to address the problem of learning multiple disjoint subgraphs which do not enable full propagation of evidence. A novel hybrid structure learning algorithm is presented in this paper for this purpose, called SaiyanH. The results show that the algorithm discovers satisfactorily accurate connected DAGs in cases where all other algorithms produce multiple disjoint subgraphs for dependent variables. This problem is highly prevalent in cases where the sample size of the input data is low with respect to the dimensionality of the model, which is often the case when working with real data. Based on six case studies, five different sample sizes, three different evaluation metrics, and other state-of-the-art or well-established constraint-based, score-based and hybrid learning algorithms, the results rank SaiyanH 4th out of 13 algorithms for overall performance.

Asian Handicap football betting with Rating-based Hybrid Bayesian Networks

Despite the massive popularity of the Asian Handicap (AH) football betting market, it has not been adequately studied by the relevant literature. This paper combines rating systems with hybrid Bayesian networks and presents the first published model specifically developed for prediction and assessment of the AH betting market. The results are based on 13 English Premier League seasons and are compared to the traditional 1X2 market. Different betting situations have been examined including a) both average and maximum (best available) market odds, b) all possible betting decision thresholds between predicted and published odds, c) optimisations for both return-on-investment and profit, and d) simple stake adjustments to investigate how the variance of returns changes when targeting equivalent profit in both 1X2 and AH markets. While the AH market is found to share the inefficiencies of the traditional 1X2 market, the findings reveal both interesting differences as well as similarities between the two.

Simpson's Paradox and the implications for medical trials

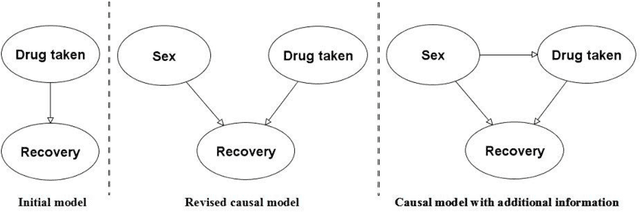
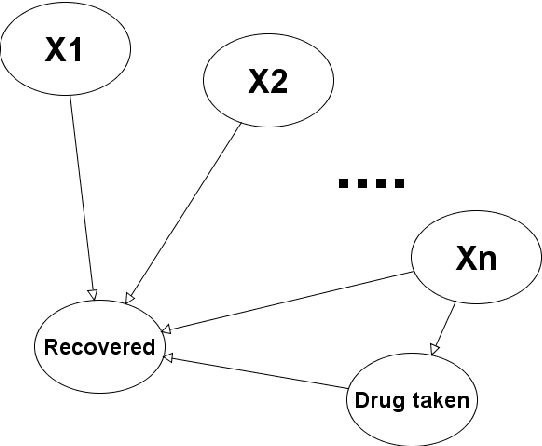
This paper describes Simpson's paradox, and explains its serious implications for randomised control trials. In particular, we show that for any number of variables we can simulate the result of a controlled trial which uniformly points to one conclusion (such as 'drug is effective') for every possible combination of the variable states, but when a previously unobserved confounding variable is included every possible combination of the variables state points to the opposite conclusion ('drug is not effective'). In other words no matter how many variables are considered, and no matter how 'conclusive' the result, one cannot conclude the result is truly 'valid' since there is theoretically an unobserved confounding variable that could completely reverse the result.

Evaluating structure learning algorithms with a balanced scoring function

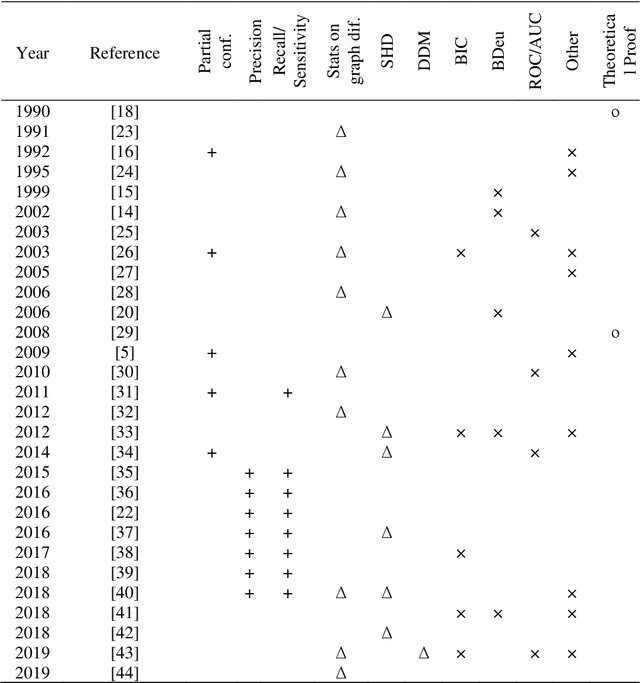
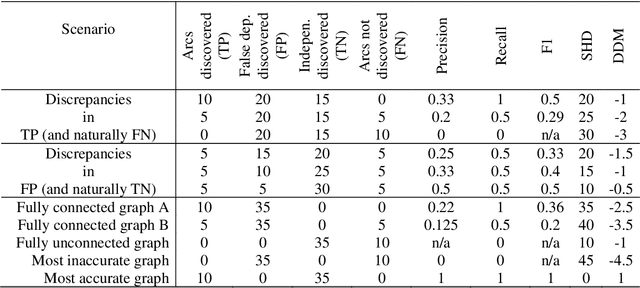
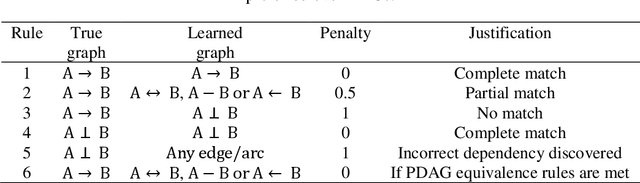
Several structure learning algorithms have been proposed towards discovering causal or Bayesian Network (BN) graphs, which is a particularly challenging problem in AI. The performance of these algorithms is evaluated based on the relationship the learned graph has with respect to the ground truth graph. However, there is no agreed scoring function to determine this relationship. Moreover, this paper shows that the commonly used metrics tend to be biased in favour of graphs that minimise the number of edges. The evaluation bias is inconsistent and may lead to evaluating graphs with no edges as superior to graphs with varying numbers of correct and incorrect edges; implying that graphs that minimise edges are often favoured over more complex graphs due to bias rather than overall accuracy. While graphs that are less complex are often desirable, the current metrics encourage algorithms to optimise for simplicity, and to discover graphs with a limited number of edges that do not enable full propagation of evidence. This paper proposes a Balanced Scoring Function (BSF) that eliminates this bias by adjusting the reward function based on the difficulty of discovering an edge, or no edge, proportional to their occurrence rate in the ground truth graph. The BSF score can be used in conjunction with other traditional metrics to provide an alternative and unbiased assessment about the capability of structure learning algorithms in discovering causal or BN graphs.