Evaluating structure learning algorithms with a balanced scoring function

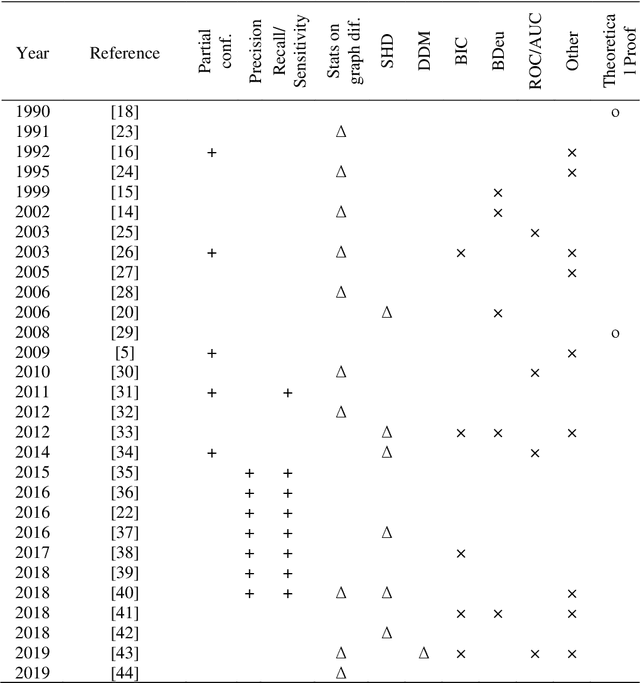
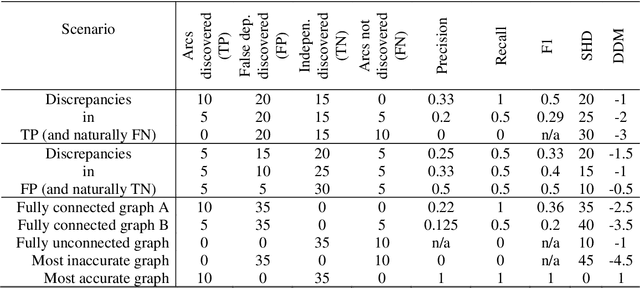
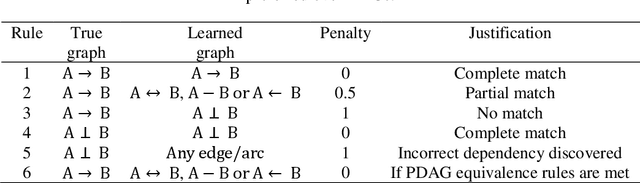
Several structure learning algorithms have been proposed towards discovering causal or Bayesian Network (BN) graphs, which is a particularly challenging problem in AI. The performance of these algorithms is evaluated based on the relationship the learned graph has with respect to the ground truth graph. However, there is no agreed scoring function to determine this relationship. Moreover, this paper shows that the commonly used metrics tend to be biased in favour of graphs that minimise the number of edges. The evaluation bias is inconsistent and may lead to evaluating graphs with no edges as superior to graphs with varying numbers of correct and incorrect edges; implying that graphs that minimise edges are often favoured over more complex graphs due to bias rather than overall accuracy. While graphs that are less complex are often desirable, the current metrics encourage algorithms to optimise for simplicity, and to discover graphs with a limited number of edges that do not enable full propagation of evidence. This paper proposes a Balanced Scoring Function (BSF) that eliminates this bias by adjusting the reward function based on the difficulty of discovering an edge, or no edge, proportional to their occurrence rate in the ground truth graph. The BSF score can be used in conjunction with other traditional metrics to provide an alternative and unbiased assessment about the capability of structure learning algorithms in discovering causal or BN graphs.