Anne Gael Manegueu
Generalized non-stationary bandits
Feb 02, 2021Abstract:In this paper, we study a non-stationary stochastic bandit problem, which generalizes the switching bandit problem. On top of the switching bandit problem (\textbf{Case a}), we are interested in three concrete examples: (\textbf{b}) the means of the arms are local polynomials, (\textbf{c}) the means of the arms are locally smooth, and (\textbf{d}) the gaps of the arms have a bounded number of inflexion points and where the highest arm mean cannot vary too much in a short range. These three settings are very different, but have in common the following: (i) the number of similarly-sized level sets of the logarithm of the gaps can be controlled, and (ii) the highest mean has a limited number of abrupt changes, and otherwise has limited variations. We propose a single algorithm in this general setting, that in particular solves in an efficient and unified way the four problems (a)-(d) mentioned.
Stochastic bandits with arm-dependent delays
Jun 18, 2020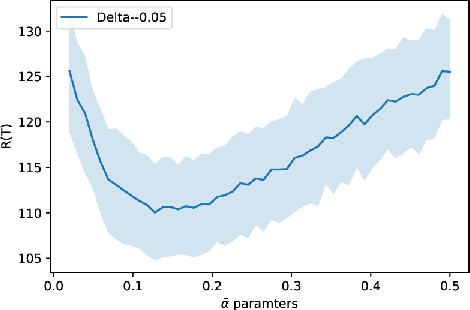

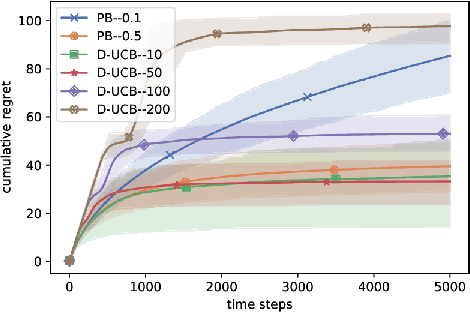
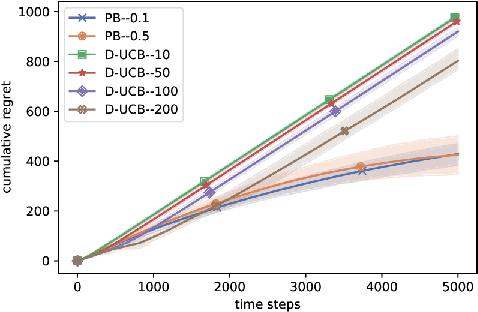
Abstract:Significant work has been recently dedicated to the stochastic delayed bandit setting because of its relevance in applications. The applicability of existing algorithms is however restricted by the fact that strong assumptions are often made on the delay distributions, such as full observability, restrictive shape constraints, or uniformity over arms. In this work, we weaken them significantly and only assume that there is a bound on the tail of the delay. In particular, we cover the important case where the delay distributions vary across arms, and the case where the delays are heavy-tailed. Addressing these difficulties, we propose a simple but efficient UCB-based algorithm called the PatientBandits. We provide both problems-dependent and problems-independent bounds on the regret as well as performance lower bounds.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge