KALAM: toolKit for Automating high-Level synthesis of Analog computing systeMs

Diverse computing paradigms have emerged to meet the growing needs for intelligent energy-efficient systems. The Margin Propagation (MP) framework, being one such initiative in the analog computing domain, stands out due to its scalability across biasing conditions, temperatures, and diminishing process technology nodes. However, the lack of digital-like automation tools for designing analog systems (including that of MP analog) hinders their adoption for designing large systems. The inherent scalability and modularity of MP systems present a unique opportunity in this regard. This paper introduces KALAM (toolKit for Automating high-Level synthesis of Analog computing systeMs), which leverages factor graphs as the foundational paradigm for synthesizing MP-based analog computing systems. Factor graphs are the basis of various signal processing tasks and, when coupled with MP, can be used to design scalable and energy-efficient analog signal processors. Using Python scripting language, the KALAM automation flow translates an input factor graph to its equivalent SPICE-compatible circuit netlist that can be used to validate the intended functionality. KALAM also allows the integration of design optimization strategies such as precision tuning, variable elimination, and mathematical simplification. We demonstrate KALAM's versatility for tasks such as Bayesian inference, Low-Density Parity Check (LDPC) decoding, and Artificial Neural Networks (ANN). Simulation results of the netlists align closely with software implementations, affirming the efficacy of our proposed automation tool.

Margin Propagation based XOR-SAT Solvers for Decoding of LDPC Codes

Decoding of Low-Density Parity Check (LDPC) codes can be viewed as a special case of XOR-SAT problems, for which low-computational complexity bit-flipping algorithms have been proposed in the literature. However, a performance gap exists between the bit-flipping LDPC decoding algorithms and the benchmark LDPC decoding algorithms, such as the Sum-Product Algorithm (SPA). In this paper, we propose an XOR-SAT solver using log-sum-exponential functions and demonstrate its advantages for LDPC decoding. This is then approximated using the Margin Propagation formulation to attain a low-complexity LDPC decoder. The proposed algorithm uses soft information to decide the bit-flips that maximize the number of parity check constraints satisfied over an optimization function. The proposed solver can achieve results that are within $0.1$dB of the Sum-Product Algorithm for the same number of code iterations. It is also at least 10x lesser than other Gradient-Descent Bit Flipping decoding algorithms, which are also bit-flipping algorithms based on optimization functions. The approximation using the Margin Propagation formulation does not require any multipliers, resulting in significantly lower computational complexity than other soft-decision Bit-Flipping LDPC decoders.

Theory and Implementation of Process and Temperature Scalable Shape-based CMOS Analog Circuits

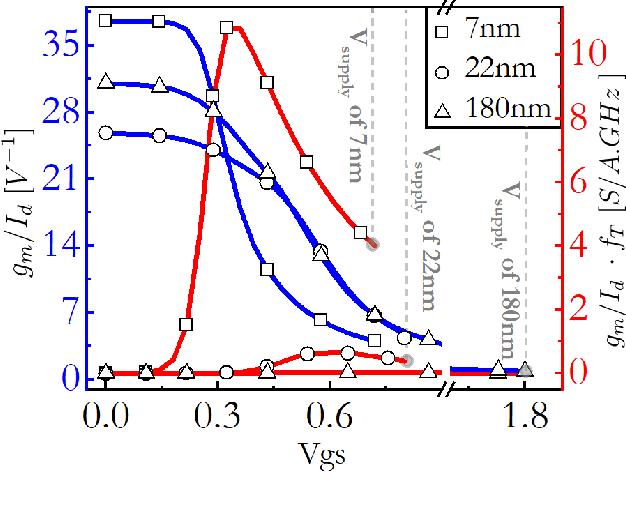
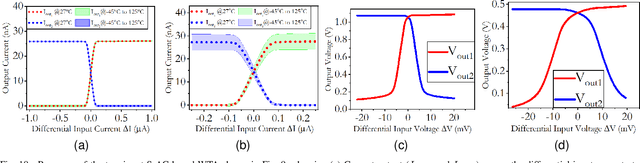
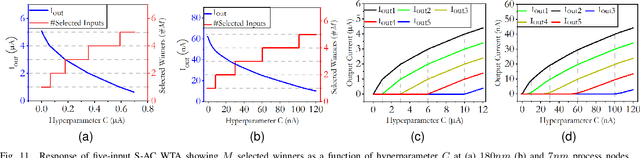
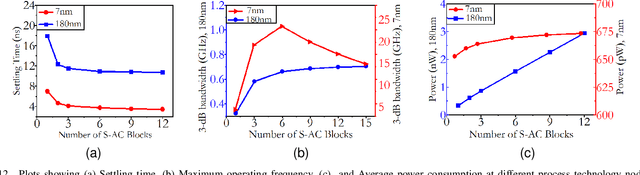
Analog computing is attractive to its digital counterparts due to its potential for achieving high compute density and energy efficiency. However, the device-to-device variability and challenges in porting existing designs to advance process nodes have posed a major hindrance in harnessing the full potential of analog computations for Machine Learning (ML) applications. This work proposes a novel analog computing framework for designing an analog ML processor similar to that of a digital design - where the designs can be scaled and ported to advanced process nodes without architectural changes. At the core of our work lies shape-based analog computing (S-AC). It utilizes device primitives to yield a robust proto-function through which other non-linear shapes can be derived. S-AC paradigm also allows the user to trade off computational precision with silicon circuit area and power. Thus allowing users to build a truly power-efficient and scalable analog architecture where the same synthesized analog circuit can operate across different biasing regimes of transistors and simultaneously scale across process nodes. As a proof of concept, we show the implementation of commonly used mathematical functions for carrying standard ML tasks in both planar CMOS 180nm and FinFET 7nm process nodes. The synthesized Shape-based ML architecture has been demonstrated for its classification accuracy on standard data sets at different process nodes.