Nesterov Meets Optimism: Rate-Optimal Optimistic-Gradient-Based Method for Stochastic Bilinearly-Coupled Minimax Optimization

We provide a novel first-order optimization algorithm for bilinearly-coupled strongly-convex-concave minimax optimization called the AcceleratedGradient OptimisticGradient (AG-OG). The main idea of our algorithm is to leverage the structure of the considered minimax problem and operates Nesterov's acceleration on the individual part and optimistic gradient on the coupling part of the objective. We motivate our method by showing that its continuous-time dynamics corresponds to an organic combination of the dynamics of optimistic gradient and of Nesterov's acceleration. By discretizing the dynamics we conclude polynomial convergence behavior in discrete time. Further enhancement of AG-OG with proper restarting allows us to achieve rate-optimal (up to a constant) convergence rates with respect to the conditioning of the coupling and individual parts, which results in the first single-call algorithm achieving improved convergence in the deterministic setting and rate-optimality in the stochastic setting under bilinearly coupled minimax problem sets.

A General Framework for Sample-Efficient Function Approximation in Reinforcement Learning

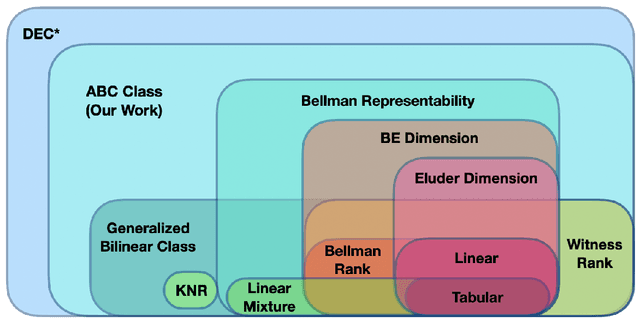
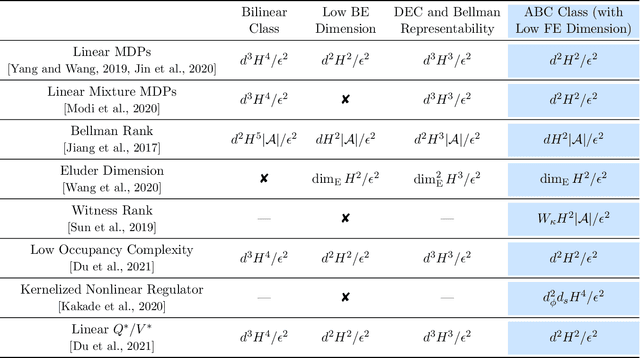
With the increasing need for handling large state and action spaces, general function approximation has become a key technique in reinforcement learning (RL). In this paper, we propose a general framework that unifies model-based and model-free RL, and an Admissible Bellman Characterization (ABC) class that subsumes nearly all Markov Decision Process (MDP) models in the literature for tractable RL. We propose a novel estimation function with decomposable structural properties for optimization-based exploration and the functional eluder dimension as a complexity measure of the ABC class. Under our framework, a new sample-efficient algorithm namely OPtimization-based ExploRation with Approximation (OPERA) is proposed, achieving regret bounds that match or improve over the best-known results for a variety of MDP models. In particular, for MDPs with low Witness rank, under a slightly stronger assumption, OPERA improves the state-of-the-art sample complexity results by a factor of $dH$. Our framework provides a generic interface to design and analyze new RL models and algorithms.