Automated Machine Learning via ADMM

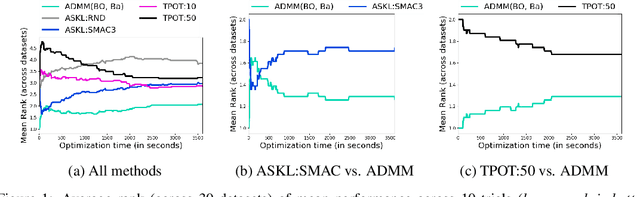
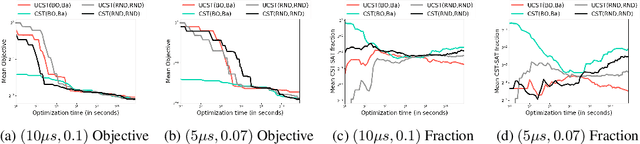
We study the automated machine learning (AutoML) problem of jointly selecting appropriate algorithms from an algorithm portfolio as well as optimizing their hyper-parameters for certain learning tasks. The main challenges include a) the coupling between algorithm selection and hyper-parameter optimization (HPO), and b) the black-box optimization nature of the problem where the optimizer cannot access the gradients of the loss function but may query function values. To circumvent these difficulties, we propose a new AutoML framework by leveraging the alternating direction method of multipliers (ADMM) scheme. Due to the splitting properties of ADMM, algorithm selection and HPO can be decomposed through the augmented Lagrangian function. As a result, HPO with mixed continuous and integer constraints are efficiently handled through a query-efficient Bayesian optimization approach and Euclidean projection operator that yields a closed-form solution. Algorithm selection in ADMM is naturally interpreted as a combinatorial bandit problem. The effectiveness of our proposed methodology is compared to state-of-the-art AutoML schemes such as TPOT and Auto-sklearn on numerous benchmark data sets.