DeepExtrema: A Deep Learning Approach for Forecasting Block Maxima in Time Series Data

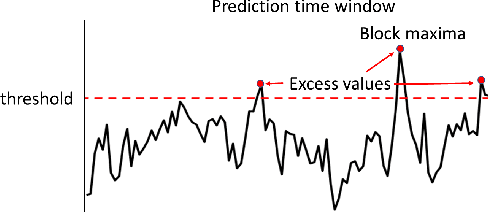
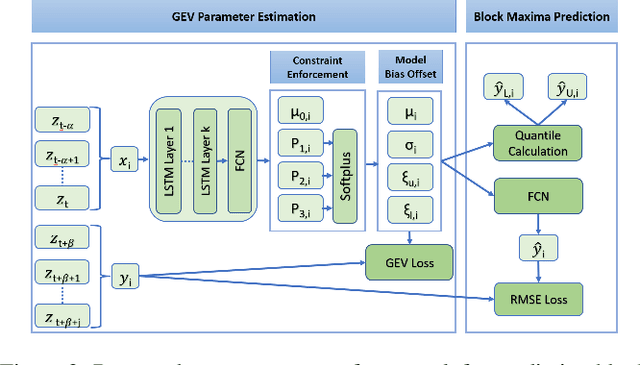
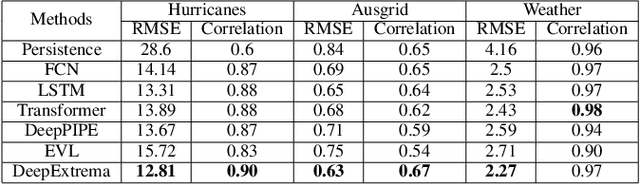
Accurate forecasting of extreme values in time series is critical due to the significant impact of extreme events on human and natural systems. This paper presents DeepExtrema, a novel framework that combines a deep neural network (DNN) with generalized extreme value (GEV) distribution to forecast the block maximum value of a time series. Implementing such a network is a challenge as the framework must preserve the inter-dependent constraints among the GEV model parameters even when the DNN is initialized. We describe our approach to address this challenge and present an architecture that enables both conditional mean and quantile prediction of the block maxima. The extensive experiments performed on both real-world and synthetic data demonstrated the superiority of DeepExtrema compared to other baseline methods.

COMET Flows: Towards Generative Modeling of Multivariate Extremes and Tail Dependence

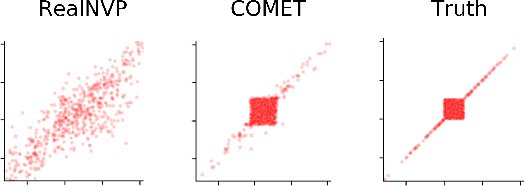
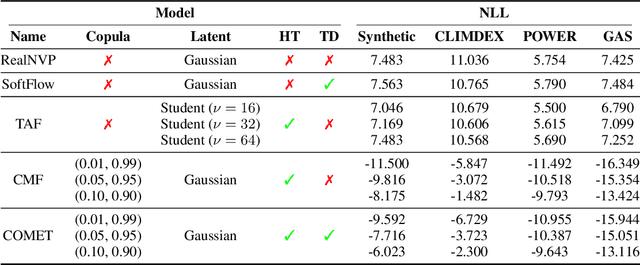
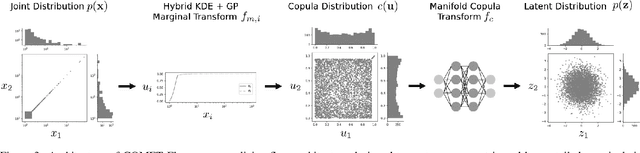
Normalizing flows, a popular class of deep generative models, often fail to represent extreme phenomena observed in real-world processes. In particular, existing normalizing flow architectures struggle to model multivariate extremes, characterized by heavy-tailed marginal distributions and asymmetric tail dependence among variables. In light of this shortcoming, we propose COMET (COpula Multivariate ExTreme) Flows, which decompose the process of modeling a joint distribution into two parts: (i) modeling its marginal distributions, and (ii) modeling its copula distribution. COMET Flows capture heavy-tailed marginal distributions by combining a parametric tail belief at extreme quantiles of the marginals with an empirical kernel density function at mid-quantiles. In addition, COMET Flows capture asymmetric tail dependence among multivariate extremes by viewing such dependence as inducing a low-dimensional manifold structure in feature space. Experimental results on both synthetic and real-world datasets demonstrate the effectiveness of COMET Flows in capturing both heavy-tailed marginals and asymmetric tail dependence compared to other state-of-the-art baseline architectures. All code is available on GitHub at https://github.com/andrewmcdonald27/COMETFlows.

Online Estimation and Coverage Control with Heterogeneous Sensing Information

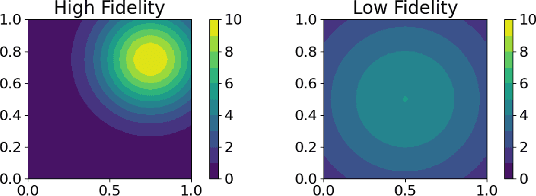
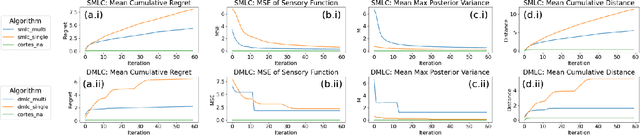
Heterogeneous multi-robot sensing systems are able to characterize physical processes more comprehensively than homogeneous systems. Access to multiple modalities of sensory data allow such systems to fuse information between complementary sources and learn richer representations of a phenomenon of interest. Often, these data are correlated but vary in fidelity, i.e., accuracy (bias) and precision (noise). Low-fidelity data may be more plentiful, while high-fidelity data may be more trustworthy. In this paper, we address the problem of multi-robot online estimation and coverage control by combining low- and high-fidelity data to learn and cover a sensory function of interest. We propose two algorithms for this task of heterogeneous learning and coverage -- namely Stochastic Sequencing of Multi-fidelity Learning and Coverage (SMLC) and Deterministic Sequencing of Multi-fidelity Learning and Coverage (DMLC) -- and prove that they converge asymptotically. In addition, we demonstrate the empirical efficacy of SMLC and DMLC through numerical simulations.

Regret Analysis of Distributed Gaussian Process Estimation and Coverage

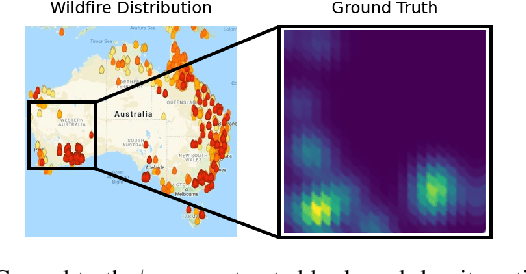
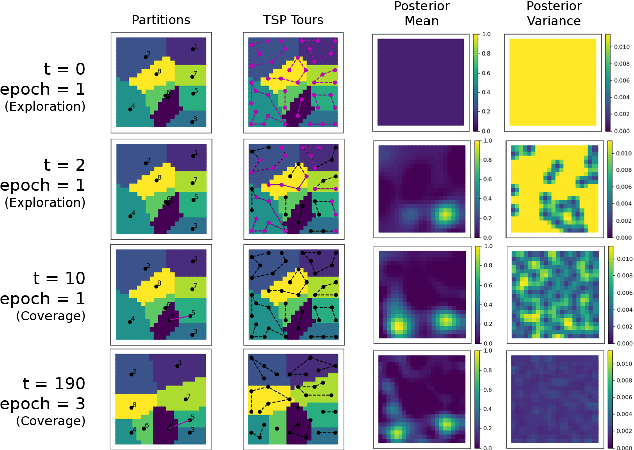
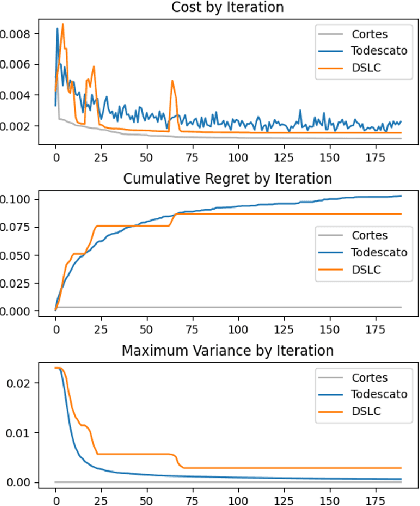
We study the problem of distributed multi-robot coverage over an unknown, nonuniform sensory field. Modeling the sensory field as a realization of a Gaussian Process and using Bayesian techniques, we devise a policy which aims to balance the tradeoff between learning the sensory function and covering the environment. We propose an adaptive coverage algorithm called Deterministic Sequencing of Learning and Coverage (DSLC) that schedules learning and coverage epochs such that its emphasis gradually shifts from exploration to exploitation while never fully ceasing to learn. Using a novel definition of coverage regret which characterizes overall coverage performance of a multi-robot team over a time horizon $T$, we analyze DSLC to provide an upper bound on expected cumulative coverage regret. Finally, we illustrate the empirical performance of the algorithm through simulations of the coverage task over an unknown distribution of wildfires.