An observer cascade for velocity and multiple line estimation

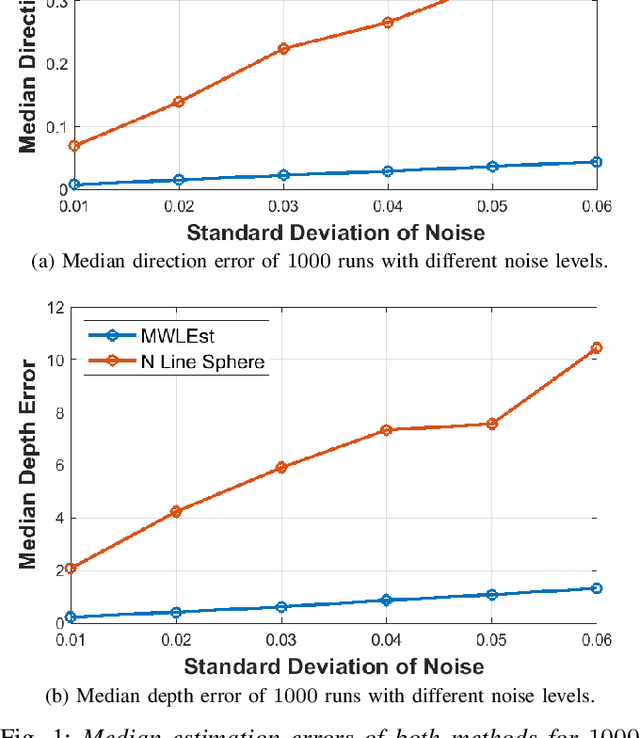
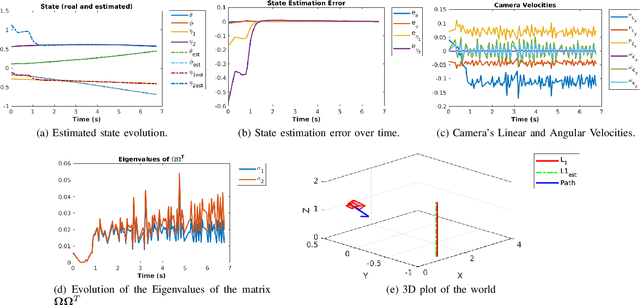
Previous incremental estimation methods consider estimating a single line, requiring as many observers as the number of lines to be mapped. This leads to the need for having at least $4N$ state variables, with $N$ being the number of lines. This paper presents the first approach for multi-line incremental estimation. Since lines are common in structured environments, we aim to exploit that structure to reduce the state space. The modeling of structured environments proposed in this paper reduces the state space to $3N + 3$ and is also less susceptible to singular configurations. An assumption the previous methods make is that the camera velocity is available at all times. However, the velocity is usually retrieved from odometry, which is noisy. With this in mind, we propose coupling the camera with an Inertial Measurement Unit (IMU) and an observer cascade. A first observer retrieves the scale of the linear velocity and a second observer for the lines mapping. The stability of the entire system is analyzed. The cascade is shown to be asymptotically stable and shown to converge in experiments with simulated data.

On Incremental Structure-from-Motion using Lines

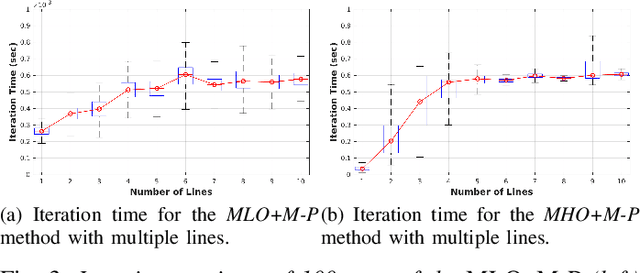
Humans tend to build environments with structure, which consists of mainly planar surfaces. From the intersection of planar surfaces arise straight lines. Lines have more degrees-of-freedom than points. Thus, line-based Structure-from-Motion (SfM) provides more information about the environment. In this paper, we present solutions for SfM using lines, namely, incremental SfM. These approaches consist of designing state observers for a camera's dynamical visual system looking at a 3D line. We start by presenting a model that uses spherical coordinates for representing the line's moment vector. We show that this parameterization has singularities, and therefore we introduce a more suitable model that considers the line's moment and shortest viewing ray. Concerning the observers, we present two different methodologies. The first uses a memory-less state-of-the-art framework for dynamic visual systems. Since the previous states of the robotic agent are accessible -- while performing the 3D mapping of the environment -- the second approach aims at exploiting the use of memory to improve the estimation accuracy and convergence speed. The two models and the two observers are evaluated in simulation and real data, where mobile and manipulator robots are used.

Active Estimation of 3D Lines in Spherical Coordinates

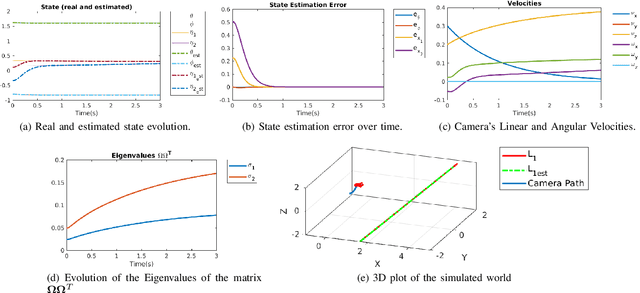
Straight lines are common features in human made environments, which makes them a frequently explored feature for control applications. Many control schemes, like Visual Servoing, require the 3D parameters of the features to be estimated. In order to obtain the 3D structure of lines, a nonlinear observer is proposed. However, to guarantee convergence, the dynamical system must be coupled with an algebraic equation. This is achieved by using spherical coordinates to represent the line's moment vector, and a change of basis, which allows to introduce the algebraic constraint directly on the system's dynamics. Finally, a control law that attempts to optimize the convergence behavior of the observer is presented. The approach is validated in simulation, and with a real robotic platform with a camera onboard.

Active Structure-from-Motion for 3D Straight Lines

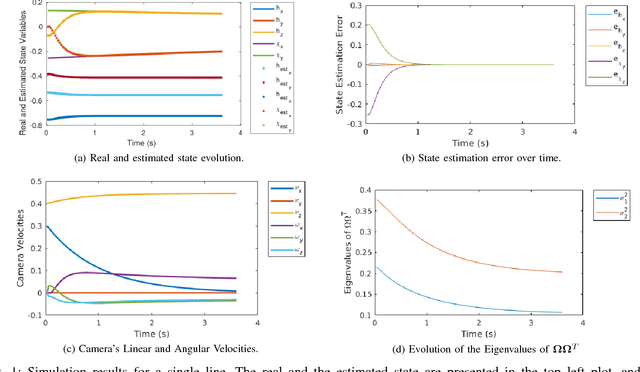
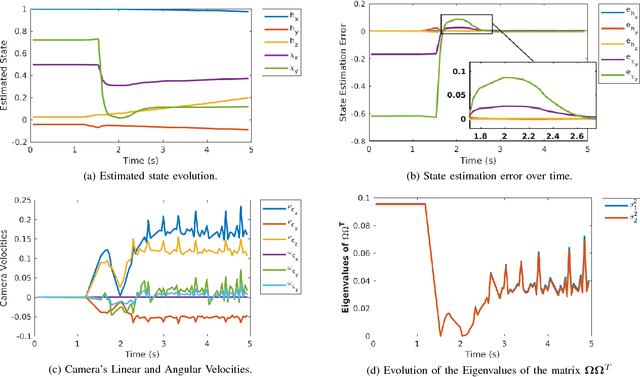
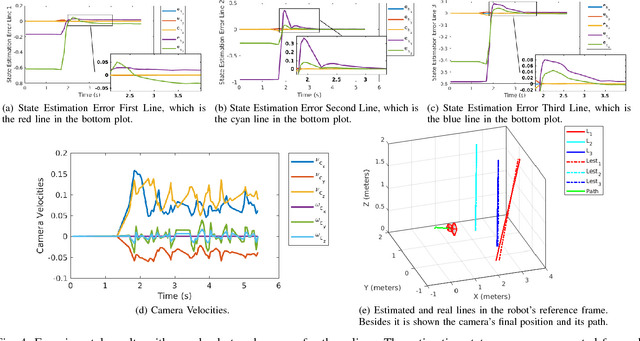
A reliable estimation of 3D parameters is a must for several applications like planning and control. Included in the latter is the Image-Based Visual Servoing, whose control scheme depends directly on 3D parameters e.g. depth of points, and depth and direction of 3D straight lines. Recently a framework for Active Structure-from-Motion was proposed, addressing the former feature type. However, straight lines were not addressed. These are 1D objects, which allow for more robust detection and tracking. In this work, the problem of Active Structure-from-Motion for 3D straight lines is addressed. An explicit representation of this type of feature is presented, and a change of variables is proposed, which allows the dynamics of the line to respect the conditions for observability of the framework. The approach is validated first in simulation for a single line, and second using a real robot. The latter set of experiments are conducted first for a single line, and then for three lines, which is the minimum required number of lines to control a 6 degree of freedom camera.