Learning Inter-Annual Flood Loss Risk Models From Historical Flood Insurance Claims and Extreme Rainfall Data

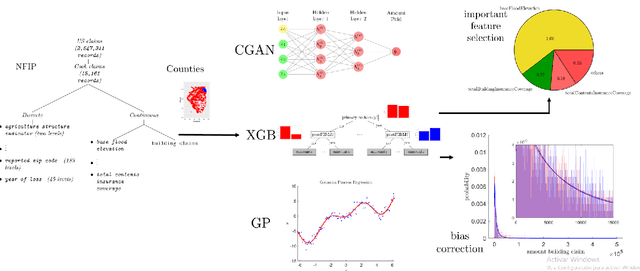
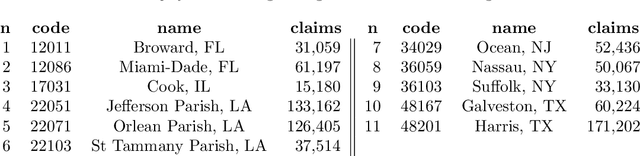
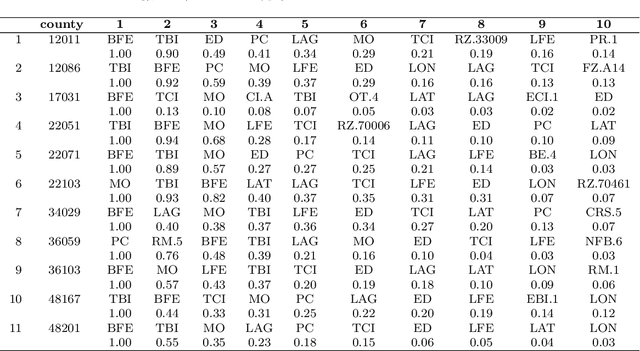
Flooding is one of the most disastrous natural hazards, responsible for substantial economic losses. A predictive model for flood-induced financial damages is useful for many applications such as climate change adaptation planning and insurance underwriting. This research assesses the predictive capability of regressors constructed on the National Flood Insurance Program (NFIP) dataset using neural networks (Conditional Generative Adversarial Networks), decision trees (Extreme Gradient Boosting), and kernel-based regressors (Gaussian Process). The assessment highlights the most informative predictors for regression. The distribution for claims amount inference is modeled with a Burr distribution permitting the introduction of a bias correction scheme and increasing the regressor's predictive capability. Aiming to study the interaction with physical variables, we incorporate Daymet rainfall estimation to NFIP as an additional predictor. A study on the coastal counties in the eight US South-West states resulted in an $R^2=0.807$. Further analysis of 11 counties with a significant number of claims in the NFIP dataset reveals that Extreme Gradient Boosting provides the best results, that bias correction significantly improves the similarity with the reference distribution, and that the rainfall predictor strengthens the regressor performance.

Downscaling Extreme Rainfall Using Physical-Statistical Generative Adversarial Learning

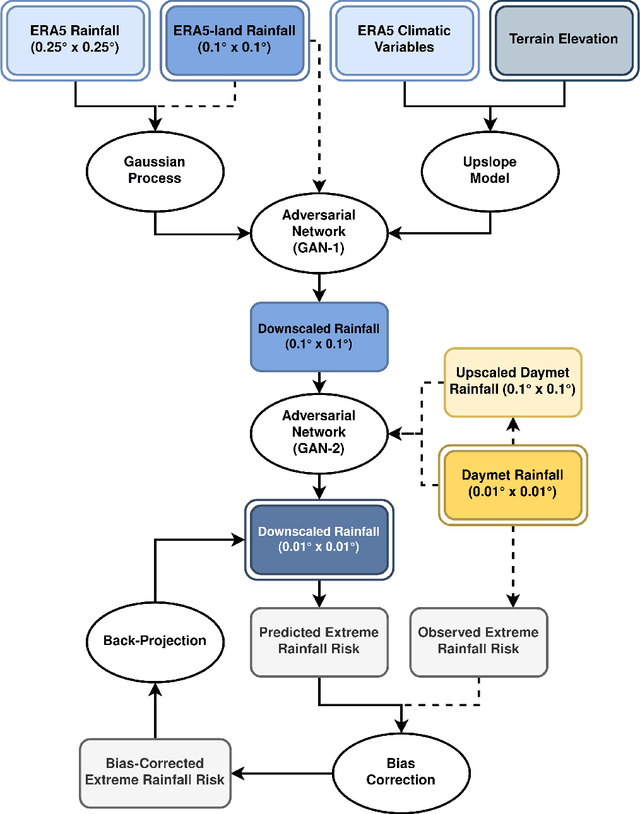
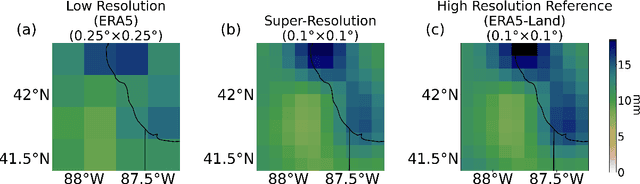
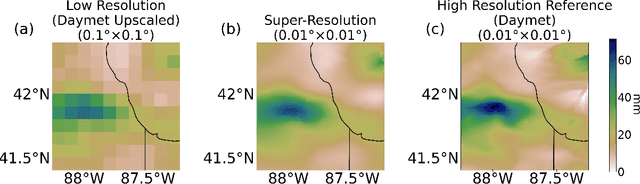
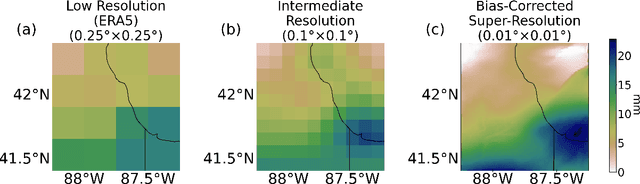
Modeling the risk of extreme weather events in a changing climate is essential for developing effective adaptation and mitigation strategies. Although the available low-resolution climate models capture different scenarios, accurate risk assessment for mitigation and adaption often demands detail that they typically cannot resolve. Here, we develop a dynamic data-driven downscaling (super-resolution) method that incorporates physics and statistics in a generative framework to learn the fine-scale spatial details of rainfall. Our method transforms coarse-resolution ($0.25^{\circ} \times 0.25^{\circ}$) climate model outputs into high-resolution ($0.01^{\circ} \times 0.01^{\circ}$) rainfall fields while efficaciously quantifying uncertainty. Results indicate that the downscaled rainfall fields closely match observed spatial fields and their risk distributions.