Asymmetric Distributed Constraint Optimization Problems

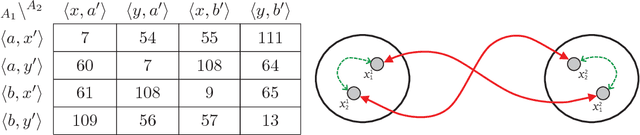
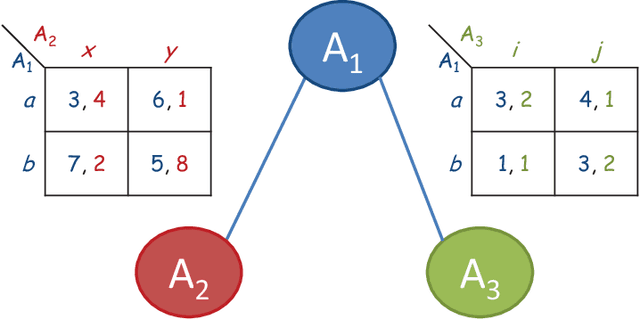
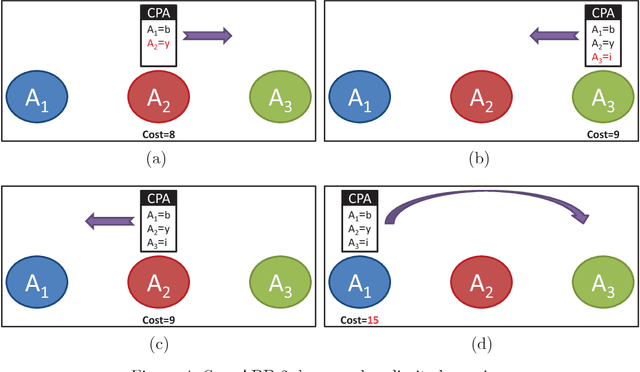
Distributed Constraint Optimization (DCOP) is a powerful framework for representing and solving distributed combinatorial problems, where the variables of the problem are owned by different agents. Many multi-agent problems include constraints that produce different gains (or costs) for the participating agents. Asymmetric gains of constrained agents cannot be naturally represented by the standard DCOP model. The present paper proposes a general framework for Asymmetric DCOPs (ADCOPs). In ADCOPs different agents may have different valuations for constraints that they are involved in. The new framework bridges the gap between multi-agent problems which tend to have asymmetric structure and the standard symmetric DCOP model. The benefits of the proposed model over previous attempts to generalize the DCOP model are discussed and evaluated. Innovative algorithms that apply to the special properties of the proposed ADCOP model are presented in detail. These include complete algorithms that have a substantial advantage in terms of runtime and network load over existing algorithms (for standard DCOPs) which use alternative representations. Moreover, standard incomplete algorithms (i.e., local search algorithms) are inapplicable to the existing DCOP representations of asymmetric constraints and when they are applied to the new ADCOP framework they often fail to converge to a local optimum and yield poor results. The local search algorithms proposed in the present paper converge to high quality solutions. The experimental evidence that is presented reveals that the proposed local search algorithms for ADCOPs achieve high quality solutions while preserving a high level of privacy.

Completeness and Performance Of The APO Algorithm

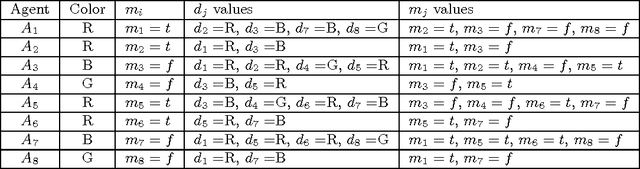
Asynchronous Partial Overlay (APO) is a search algorithm that uses cooperative mediation to solve Distributed Constraint Satisfaction Problems (DisCSPs). The algorithm partitions the search into different subproblems of the DisCSP. The original proof of completeness of the APO algorithm is based on the growth of the size of the subproblems. The present paper demonstrates that this expected growth of subproblems does not occur in some situations, leading to a termination problem of the algorithm. The problematic parts in the APO algorithm that interfere with its completeness are identified and necessary modifications to the algorithm that fix these problematic parts are given. The resulting version of the algorithm, Complete Asynchronous Partial Overlay (CompAPO), ensures its completeness. Formal proofs for the soundness and completeness of CompAPO are given. A detailed performance evaluation of CompAPO comparing it to other DisCSP algorithms is presented, along with an extensive experimental evaluation of the algorithm's unique behavior. Additionally, an optimization version of the algorithm, CompOptAPO, is presented, discussed, and evaluated.

Asynchronous Forward Bounding for Distributed COPs

A new search algorithm for solving distributed constraint optimization problems (DisCOPs) is presented. Agents assign variables sequentially and compute bounds on partial assignments asynchronously. The asynchronous bounds computation is based on the propagation of partial assignments. The asynchronous forward-bounding algorithm (AFB) is a distributed optimization search algorithm that keeps one consistent partial assignment at all times. The algorithm is described in detail and its correctness proven. Experimental evaluation shows that AFB outperforms synchronous branch and bound by many orders of magnitude, and produces a phase transition as the tightness of the problem increases. This is an analogous effect to the phase transition that has been observed when local consistency maintenance is applied to MaxCSPs. The AFB algorithm is further enhanced by the addition of a backjumping mechanism, resulting in the AFB-BJ algorithm. Distributed backjumping is based on accumulated information on bounds of all values and on processing concurrently a queue of candidate goals for the next move back. The AFB-BJ algorithm is compared experimentally to other DisCOP algorithms (ADOPT, DPOP, OptAPO) and is shown to be a very efficient algorithm for DisCOPs.