Asymmetric Distributed Constraint Optimization Problems
Paper and Code
Feb 04, 2014
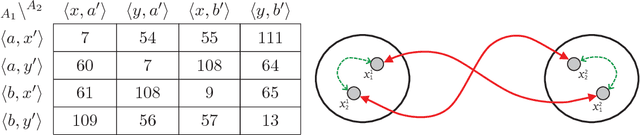
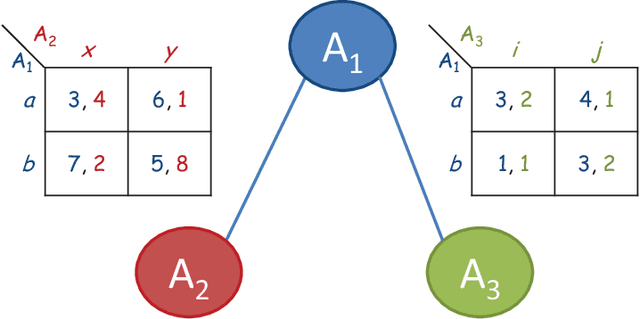
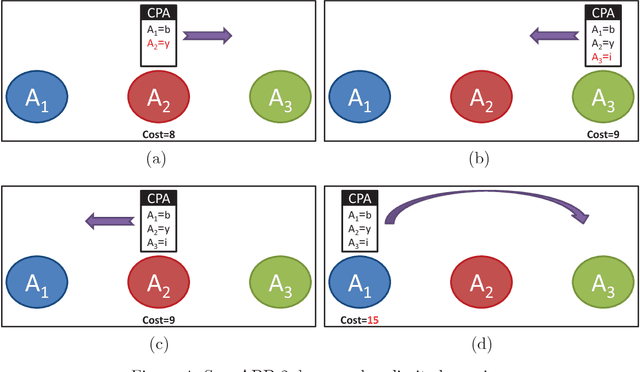
Distributed Constraint Optimization (DCOP) is a powerful framework for representing and solving distributed combinatorial problems, where the variables of the problem are owned by different agents. Many multi-agent problems include constraints that produce different gains (or costs) for the participating agents. Asymmetric gains of constrained agents cannot be naturally represented by the standard DCOP model. The present paper proposes a general framework for Asymmetric DCOPs (ADCOPs). In ADCOPs different agents may have different valuations for constraints that they are involved in. The new framework bridges the gap between multi-agent problems which tend to have asymmetric structure and the standard symmetric DCOP model. The benefits of the proposed model over previous attempts to generalize the DCOP model are discussed and evaluated. Innovative algorithms that apply to the special properties of the proposed ADCOP model are presented in detail. These include complete algorithms that have a substantial advantage in terms of runtime and network load over existing algorithms (for standard DCOPs) which use alternative representations. Moreover, standard incomplete algorithms (i.e., local search algorithms) are inapplicable to the existing DCOP representations of asymmetric constraints and when they are applied to the new ADCOP framework they often fail to converge to a local optimum and yield poor results. The local search algorithms proposed in the present paper converge to high quality solutions. The experimental evidence that is presented reveals that the proposed local search algorithms for ADCOPs achieve high quality solutions while preserving a high level of privacy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge