Wireless Federated Learning with Limited Communication and Differential Privacy

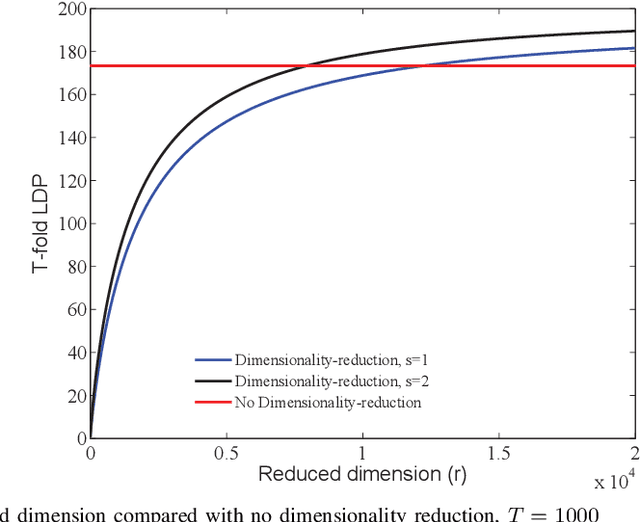
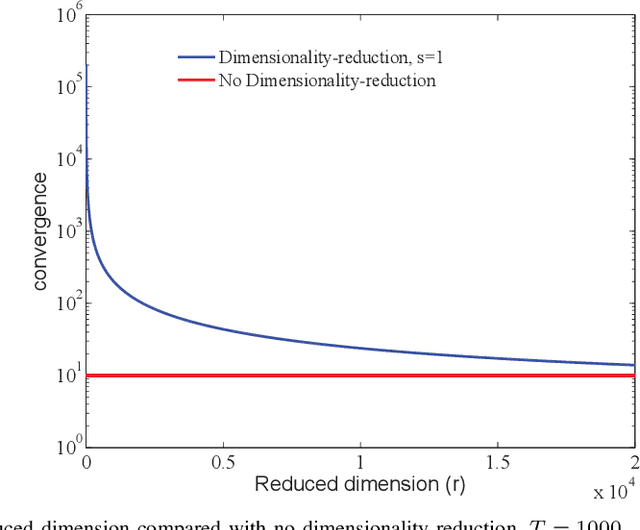
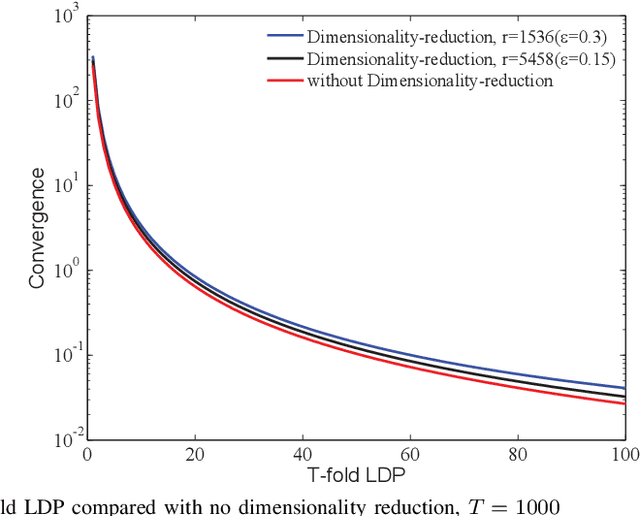
This paper investigates the role of dimensionality reduction in efficient communication and differential privacy (DP) of the local datasets at the remote users for over-the-air computation (AirComp)-based federated learning (FL) model. More precisely, we consider the FL setting in which clients are prompted to train a machine learning model by simultaneous channel-aware and limited communications with a parameter server (PS) over a Gaussian multiple-access channel (GMAC), so that transmissions sum coherently at the PS globally aware of the channel coefficients. For this setting, an algorithm is proposed based on applying federated stochastic gradient descent (FedSGD) for training the minimum of a given loss function based on the local gradients, Johnson-Lindenstrauss (JL) random projection for reducing the dimension of the local updates, and artificial noise to further aid user's privacy. For this scheme, our results show that the local DP performance is mainly improved due to injecting noise of greater variance on each dimension while keeping the sensitivity of the projected vectors unchanged. This is while the convergence rate is slowed down compared to the case without dimensionality reduction. As the performance outweighs for the slower convergence, the trade-off between privacy and convergence is higher but is shown to lessen in high-dimensional regime yielding almost the same trade-off with much less communication cost.

Efficient Federated Learning over Multiple Access Channel with Differential Privacy Constraints

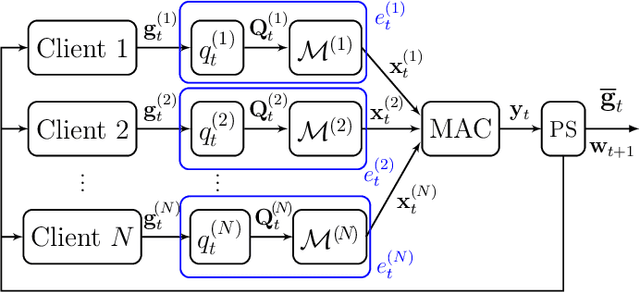
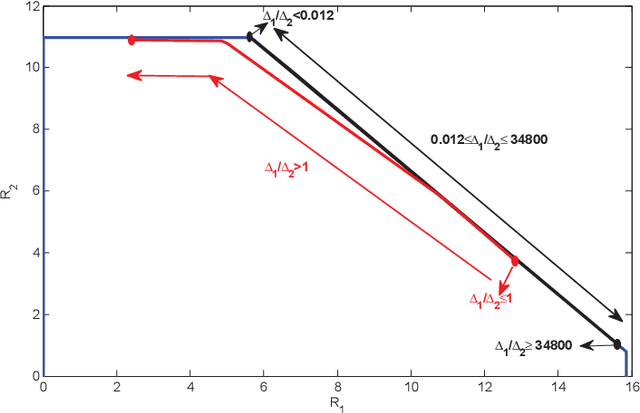
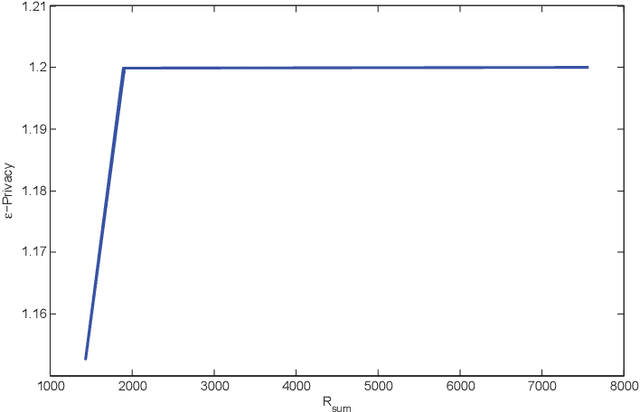
In this paper, the problem of federated learning (FL) over a multiple access channel (MAC) is considered. More precisely, we consider the FL setting in which clients are prompted to train a machine learning model by simultaneous communications with a parameter server (PS) with the aim of better utilizing the computational resources available in the network. We also consider the additional constraint in which the communication between the users and the PS is subject to a privacy constraint. To minimize the training loss while also satisfying the privacy rate constraint over the MAC channel, the distributed transmission of digital variants of stochastic gradient descents (D-DSGD) is performed by each client. Additionally, binomial noise is also added at each user to preserve the privacy of the transmission. The optimum levels of quantization in the D-DSGD and the binary noise parameters to achieve efficiency in terms of convergence are investigated, subject to privacy constraint and capacity limit of the MAC channel.