Wireless Federated Learning with Limited Communication and Differential Privacy
Paper and Code
Jun 01, 2021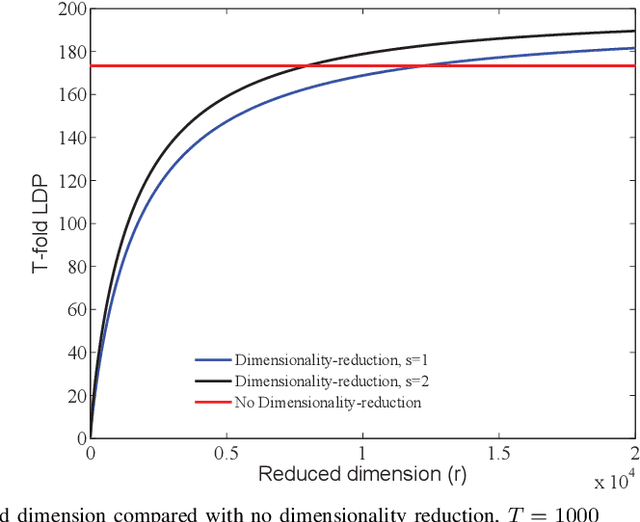
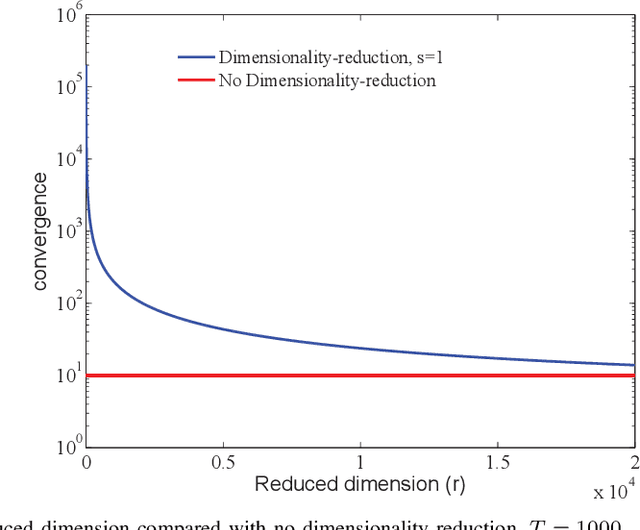
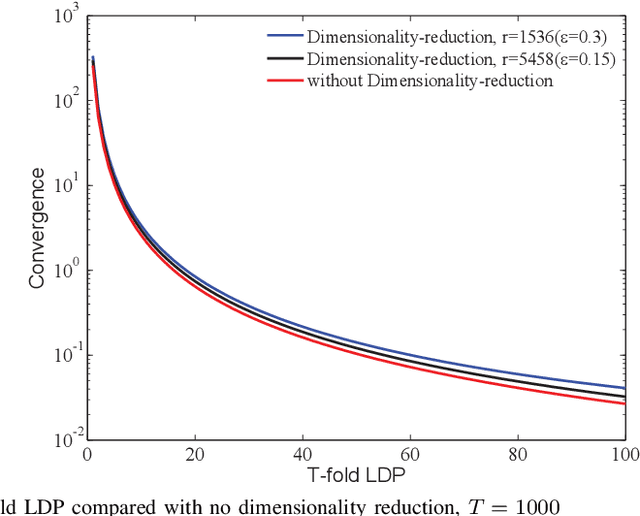
This paper investigates the role of dimensionality reduction in efficient communication and differential privacy (DP) of the local datasets at the remote users for over-the-air computation (AirComp)-based federated learning (FL) model. More precisely, we consider the FL setting in which clients are prompted to train a machine learning model by simultaneous channel-aware and limited communications with a parameter server (PS) over a Gaussian multiple-access channel (GMAC), so that transmissions sum coherently at the PS globally aware of the channel coefficients. For this setting, an algorithm is proposed based on applying federated stochastic gradient descent (FedSGD) for training the minimum of a given loss function based on the local gradients, Johnson-Lindenstrauss (JL) random projection for reducing the dimension of the local updates, and artificial noise to further aid user's privacy. For this scheme, our results show that the local DP performance is mainly improved due to injecting noise of greater variance on each dimension while keeping the sensitivity of the projected vectors unchanged. This is while the convergence rate is slowed down compared to the case without dimensionality reduction. As the performance outweighs for the slower convergence, the trade-off between privacy and convergence is higher but is shown to lessen in high-dimensional regime yielding almost the same trade-off with much less communication cost.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge