HT-LIP Model based Robust Control of Quadrupedal Robot Locomotion under Unknown Vertical Ground Motion

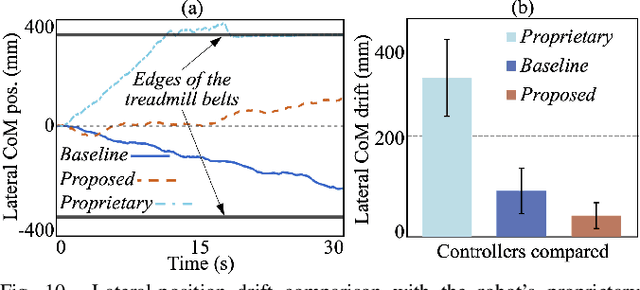
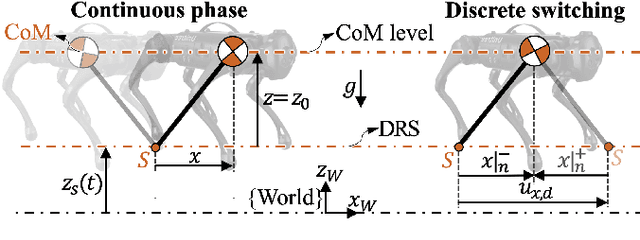
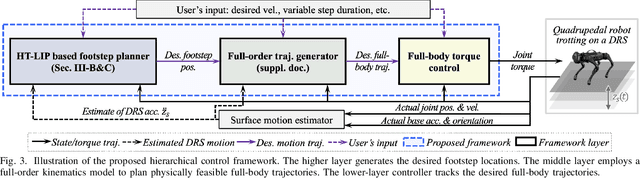
This paper presents a hierarchical control framework that enables robust quadrupedal locomotion on a dynamic rigid surface (DRS) with general and unknown vertical motions. The key novelty of the framework lies in its higher layer, which is a discrete-time, provably stabilizing footstep controller. The basis of the footstep controller is a new hybrid, time-varying, linear inverted pendulum (HT-LIP) model that is low-dimensional and accurately captures the essential robot dynamics during DRS locomotion. A new set of sufficient stability conditions are then derived to directly guide the controller design for ensuring the asymptotic stability of the HT-LIP model under general, unknown, vertical DRS motions. Further, the footstep controller is cast as a computationally efficient quadratic program that incorporates the proposed HT-LIP model and stability conditions. The middle layer takes the desired footstep locations generated by the higher layer as input to produce kinematically feasible full-body reference trajectories, which are then accurately tracked by a lower-layer torque controller. Hardware experiments on a Unitree Go1 quadrupedal robot confirm the robustness of the proposed framework under various unknown, aperiodic, vertical DRS motions and uncertainties (e.g., slippery and uneven surfaces, solid and liquid loads, and sudden pushes).

Real-Time Walking Pattern Generation of Quadrupedal Dynamic-Surface Locomotion based on a Linear Time-Varying Pendulum Model

This study introduces an analytically tractable and computationally efficient model of the legged robot dynamics associated with locomotion on a dynamic rigid surface (DRS), and develops a real-time motion planner based on the proposed model and its analytical solution. This study first theoretically extends the classical linear inverted pendulum (LIP) model from legged locomotion on a static surface to DRS locomotion, by relaxing the LIP's underlying assumption that the surface is static. The resulting model, which we call "DRS-LIP", is explicitly time-varying. After converting the DRS-LIP into Mathieu's equation, an approximate analytical solution of the DRS-LIP is obtained, which is reasonably accurate with a low computational cost. Furthermore, to illustrate the practical uses of the analytical results, they are exploited to develop a hierarchical motion planner that efficiently generates physically feasible trajectories for DRS locomotion. Finally, the effectiveness of the proposed theoretical results and motion planner is demonstrated both through PyBullet simulations and experimentally on a Laikago quadrupedal robot that walks on a rocking treadmill. The videos of simulations and hardware experiments are available at https://youtu.be/u2Q_u2pR99c.

DRS-LIP: Linear Inverted Pendulum Model for Legged Locomotion on Dynamic Rigid Surfaces

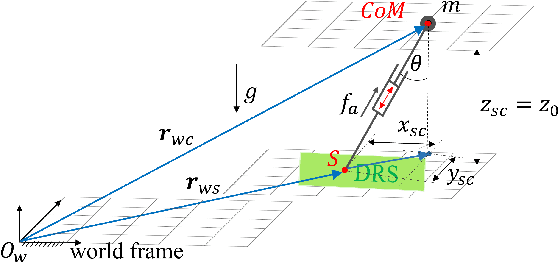
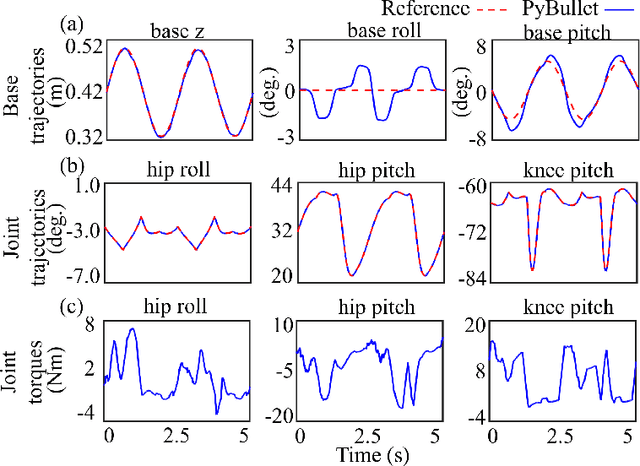
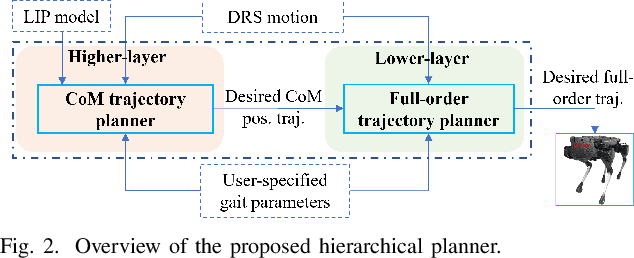
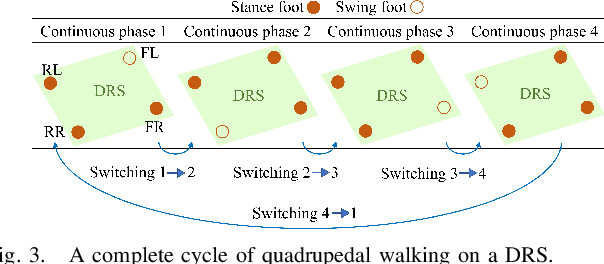
Legged robot locomotion on a dynamic rigid surface (i.e., a rigid surface moving in the inertial frame) involves complex full-order dynamics that is high-dimensional, nonlinear, and time-varying. Towards deriving an analytically tractable dynamic model, this study theoretically extends the reduced-order linear inverted pendulum (LIP) model from legged locomotion on a stationary surface to locomotion on a dynamic rigid surface (DRS). The resulting model is herein termed as DRS-LIP. Furthermore, this study introduces an approximate analytical solution of the proposed DRS-LIP that is computationally efficient with high accuracy. To illustrate the practical uses of the analytical results, they are used to develop a hierarchical planning framework that efficiently generates physically feasible trajectories for DRS locomotion. The effectiveness of the proposed theoretical results and motion planner is demonstrated both through simulations and experimentally on a Laikago quadrupedal robot that walks on a rocking treadmill.

Extended Capture Point and Optimization-based Control for Quadrupedal Robot Walking on Dynamic Rigid Surfaces

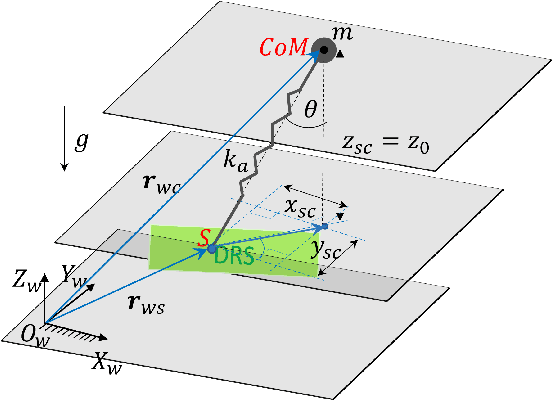
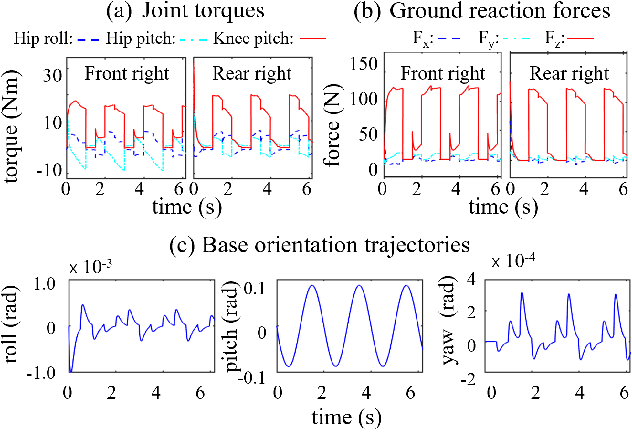
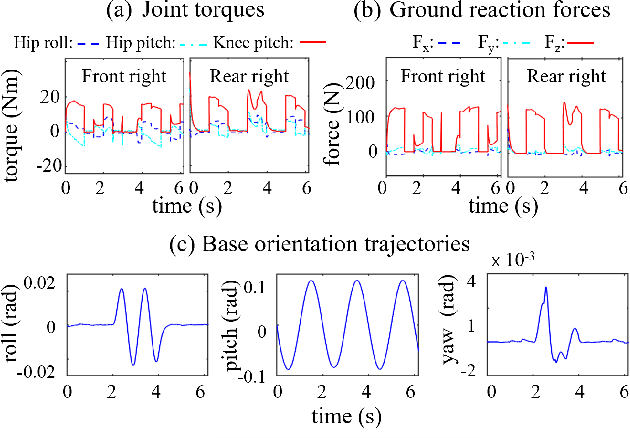
Stabilizing legged robot locomotion on a dynamic rigid surface (DRS) (i.e., rigid surface that moves in the inertial frame) is a complex planning and control problem. The complexity arises due to the hybrid nonlinear walking dynamics subject to explicitly time-varying holonomic constraints caused by the surface movement. The first main contribution of this study is the extension of the capture point from walking on a static surface to locomotion on a DRS as well as the use of the resulting capture point for online motion planning. The second main contribution is a quadratic-programming (QP) based feedback controller design that explicitly considers the DRS movement. The stability and robustness of the proposed control approach are validated through simulations of a quadrupedal robot walking on a DRS with a rocking motion. The simulation results also demonstrate the improved walking performance compared with our previous approach based on offline planning and input-output linearizing control that does not explicitly guarantee the feasibility of ground contact constraints.