Striking a Balance: An Optimal Mechanism Design for Heterogenous Differentially Private Data Acquisition for Logistic Regression

We investigate the problem of performing logistic regression on data collected from privacy-sensitive sellers. Since the data is private, sellers must be incentivized through payments to provide their data. Thus, the goal is to design a mechanism that optimizes a weighted combination of test loss, seller privacy, and payment, i.e., strikes a balance between multiple objectives of interest. We solve the problem by combining ideas from game theory, statistical learning theory, and differential privacy. The buyer's objective function can be highly non-convex. However, we show that, under certain conditions on the problem parameters, the problem can be convexified by using a change of variables. We also provide asymptotic results characterizing the buyer's test error and payments when the number of sellers becomes large. Finally, we demonstrate our ideas by applying them to a real healthcare data set.

A Weighted Generalized Coherence Approach for Sensing Matrix Design

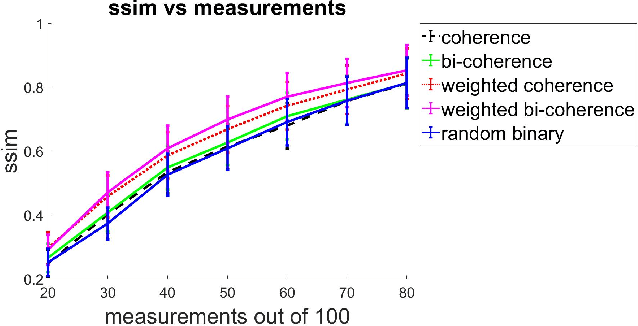
As compared to using randomly generated sensing matrices, optimizing the sensing matrix w.r.t. a carefully designed criterion is known to lead to better quality signal recovery given a set of compressive measurements. In this paper, we propose generalizations of the well-known mutual coherence criterion for optimizing sensing matrices starting from random initial conditions. We term these generalizations as bi-coherence or tri-coherence and they are based on a criterion that discourages any one column of the sensing matrix from being close to a sparse linear combination of other columns. We also incorporate training data to further improve the sensing matrices through weighted coherence, weighted bi-coherence, or weighted tri-coherence criteria, which assign weights to sensing matrix columns as per their importance. An algorithm is also presented to solve the optimization problems. Finally, the effectiveness of the proposed algorithm is demonstrated through empirical results.