A Sublinear Algorithm for Path Feasibility Among Rectangular Obstacles

The problem of finding a path between two points while avoiding obstacles is critical in robotic path planning. We focus on the feasibility problem: determining whether such a path exists. We model the robot as a query-specific rectangular object capable of moving parallel to its sides. The obstacles are axis-aligned, rectangular, and may overlap. Most previous works only consider nondisjoint rectangular objects and point-sized or statically sized robots. Our approach introduces a novel technique leveraging generalized Gabriel graphs and constructs a data structure to facilitate online queries regarding path feasibility with varying robot sizes in sublinear time. To efficiently handle feasibility queries, we propose an online algorithm utilizing sweep line to construct a generalized Gabriel graph under the $L_\infty$ norm, capturing key gap constraints between obstacles. We utilize a persistent disjoint-set union data structure to efficiently determine feasibility queries in $\mathcal{O}(\log n)$ time and $\mathcal{O}(n)$ total space.

Learning to Bridge the Gap: Efficient Novelty Recovery with Planning and Reinforcement Learning

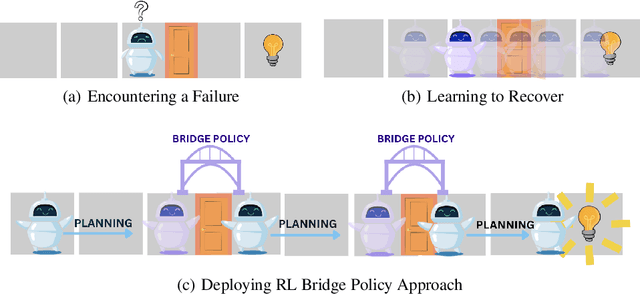
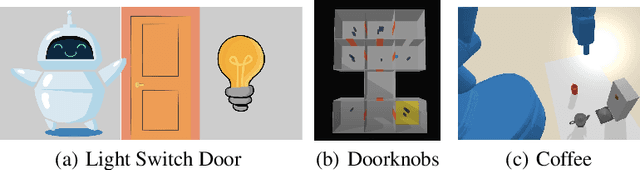
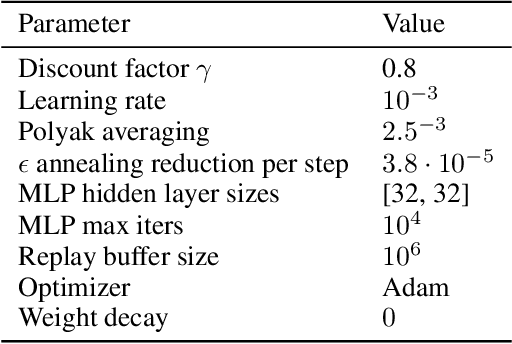
The real world is unpredictable. Therefore, to solve long-horizon decision-making problems with autonomous robots, we must construct agents that are capable of adapting to changes in the environment during deployment. Model-based planning approaches can enable robots to solve complex, long-horizon tasks in a variety of environments. However, such approaches tend to be brittle when deployed into an environment featuring a novel situation that their underlying model does not account for. In this work, we propose to learn a ``bridge policy'' via Reinforcement Learning (RL) to adapt to such novelties. We introduce a simple formulation for such learning, where the RL problem is constructed with a special ``CallPlanner'' action that terminates the bridge policy and hands control of the agent back to the planner. This allows the RL policy to learn the set of states in which querying the planner and following the returned plan will achieve the goal. We show that this formulation enables the agent to rapidly learn by leveraging the planner's knowledge to avoid challenging long-horizon exploration caused by sparse reward. In experiments across three different simulated domains of varying complexity, we demonstrate that our approach is able to learn policies that adapt to novelty more efficiently than several baselines, including a pure RL baseline. We also demonstrate that the learned bridge policy is generalizable in that it can be combined with the planner to enable the agent to solve more complex tasks with multiple instances of the encountered novelty.