Quantum Semi-Supervised Kernel Learning

Quantum computing leverages quantum effects to build algorithms that are faster then their classical variants. In machine learning, for a given model architecture, the speed of training the model is typically determined by the size of the training dataset. Thus, quantum machine learning methods have the potential to facilitate learning using extremely large datasets. While the availability of data for training machine learning models is steadily increasing, oftentimes it is much easier to collect feature vectors that to obtain the corresponding labels. One of the approaches for addressing this issue is to use semi-supervised learning, which leverages not only the labeled samples, but also unlabeled feature vectors. Here, we present a quantum machine learning algorithm for training Semi-Supervised Kernel Support Vector Machines. The algorithm uses recent advances in quantum sample-based Hamiltonian simulation to extend the existing Quantum LS-SVM algorithm to handle the semi-supervised term in the loss. Through a theoretical study of the algorithm's computational complexity, we show that it maintains the same speedup as the fully-supervised Quantum LS-SVM.

CS-NLP team at SemEval-2020 Task 4: Evaluation of State-of-the-artNLP Deep Learning Architectures on Commonsense Reasoning Task

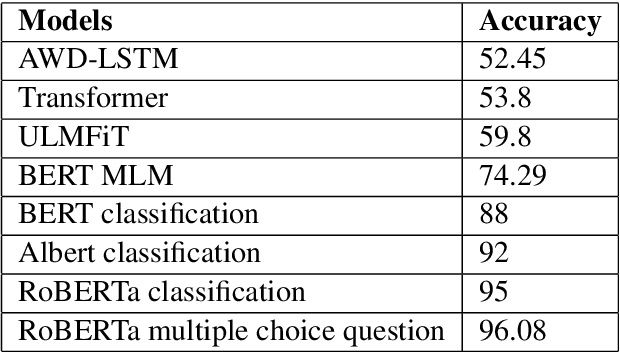
In this paper, we investigate a commonsense inference task that unifies natural language understanding and commonsense reasoning. We describe our attempt at SemEval-2020 Task 4competition: Commonsense Validation and Explanation (ComVE) challenge. We discuss several state-of-the-art deep learning architectures for this challenge. Our system uses prepared labeled textual datasets that were manually curated for three different natural language inference tasks.The goal of the first subtask is to test whether a model can distinguish between natural language statements that make sense and those that do not make sense. We compare the performance of several language models and fine-tuned classifiers. Then, we propose a method inspired by question/answering tasks to treat a classification problem as a multiple choice question task to boost the performance of our experimental results (96.06%), which is significantly better than the baseline. For the second subtask, which is to select the reason why a statement does not make sense, we stand within the first six teams (93.7%) among 27 participants with very competitive results.

word2ket: Space-efficient Word Embeddings inspired by Quantum Entanglement

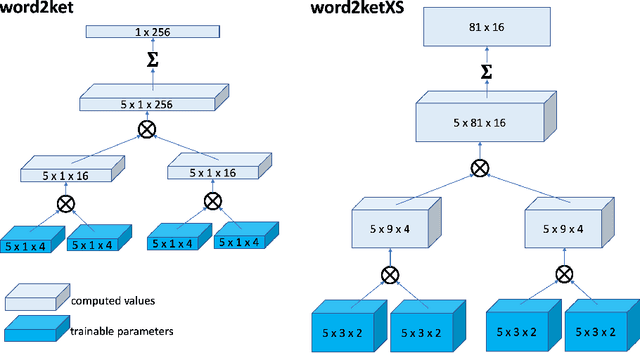
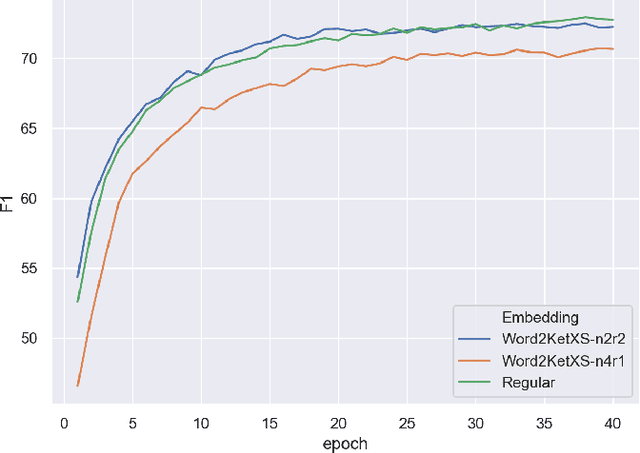
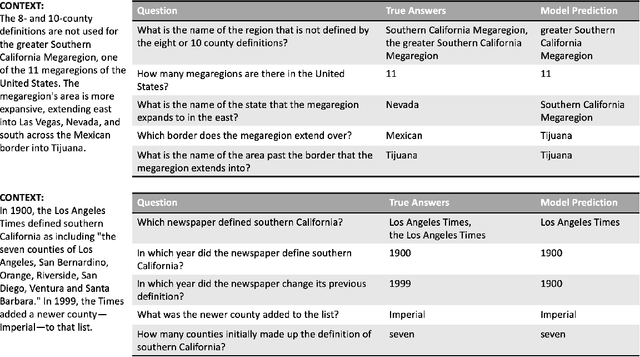
Deep learning natural language processing models often use vector word embeddings, such as word2vec or GloVe, to represent words. A discrete sequence of words can be much more easily integrated with downstream neural layers if it is represented as a sequence of continuous vectors. Also, semantic relationships between words, learned from a text corpus, can be encoded in the relative configurations of the embedding vectors. However, storing and accessing embedding vectors for all words in a dictionary requires large amount of space, and may stain systems with limited GPU memory. Here, we used approaches inspired by quantum computing to propose two related methods, {\em word2ket} and {\em word2ketXS}, for storing word embedding matrix during training and inference in a highly efficient way. Our approach achieves a hundred-fold or more reduction in the space required to store the embeddings with almost no relative drop in accuracy in practical natural language processing tasks.

Combinatorial Losses through Generalized Gradients of Integer Linear Programs

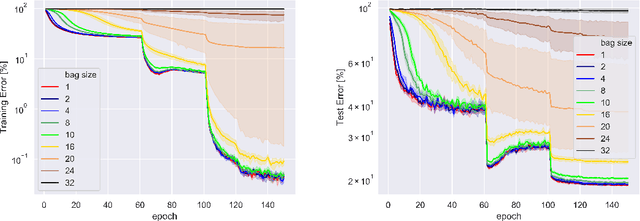
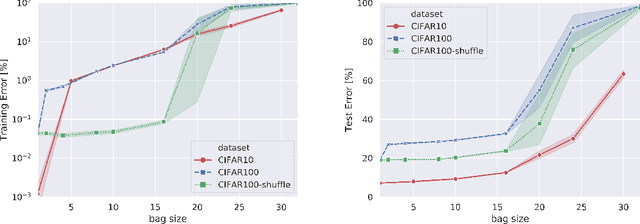
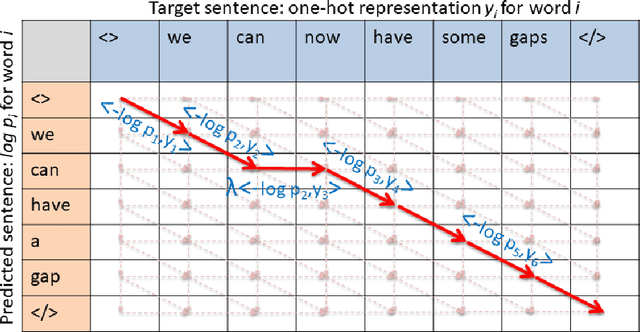
When samples have internal structure, we often see a mismatch between the objective optimized during training and the model's goal during inference. For example, in sequence-to-sequence modeling we are interested in high-quality translated sentences, but training typically uses maximum likelihood at the word level. Learning to recognize individual faces from group photos, each captioned with the correct but unordered list of people in it, is another example where a mismatch between training and inference objectives occurs. In both cases, the natural training-time loss would involve a combinatorial problem -- dynamic programming-based global sequence alignment and weighted bipartite graph matching, respectively -- but solutions to combinatorial problems are not differentiable with respect to their input parameters, so surrogate, differentiable losses are used instead. Here, we show how to perform gradient descent over combinatorial optimization algorithms that involve continuous parameters, for example edge weights, and can be efficiently expressed as integer, linear, or mixed-integer linear programs. We demonstrate usefulness of gradient descent over combinatorial optimization in sequence-to-sequence modeling using differentiable encoder-decoder architecture with softmax or Gumbel-softmax, and in weakly supervised learning involving a convolutional, residual feed-forward network for image classification.