Combinatorial Losses through Generalized Gradients of Integer Linear Programs
Paper and Code
Oct 18, 2019
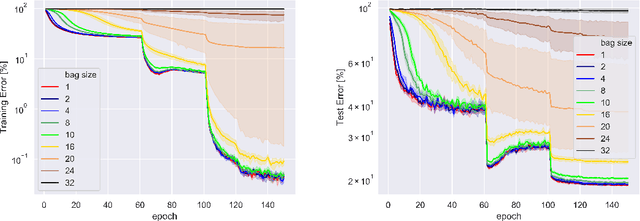
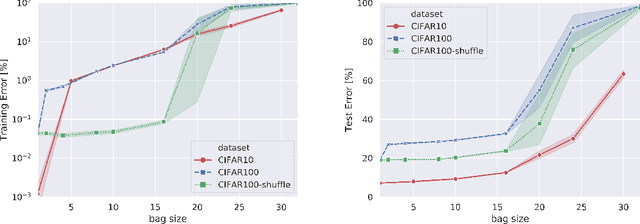
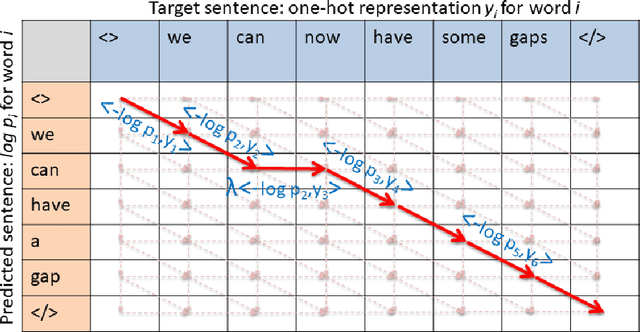
When samples have internal structure, we often see a mismatch between the objective optimized during training and the model's goal during inference. For example, in sequence-to-sequence modeling we are interested in high-quality translated sentences, but training typically uses maximum likelihood at the word level. Learning to recognize individual faces from group photos, each captioned with the correct but unordered list of people in it, is another example where a mismatch between training and inference objectives occurs. In both cases, the natural training-time loss would involve a combinatorial problem -- dynamic programming-based global sequence alignment and weighted bipartite graph matching, respectively -- but solutions to combinatorial problems are not differentiable with respect to their input parameters, so surrogate, differentiable losses are used instead. Here, we show how to perform gradient descent over combinatorial optimization algorithms that involve continuous parameters, for example edge weights, and can be efficiently expressed as integer, linear, or mixed-integer linear programs. We demonstrate usefulness of gradient descent over combinatorial optimization in sequence-to-sequence modeling using differentiable encoder-decoder architecture with softmax or Gumbel-softmax, and in weakly supervised learning involving a convolutional, residual feed-forward network for image classification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge