Risk Analysis and Design Against Adversarial Actions

Learning models capable of providing reliable predictions in the face of adversarial actions has become a central focus of the machine learning community in recent years. This challenge arises from observing that data encountered at deployment time often deviate from the conditions under which the model was trained. In this paper, we address deployment-time adversarial actions and propose a versatile, well-principled framework to evaluate the model's robustness against attacks of diverse types and intensities. While we initially focus on Support Vector Regression (SVR), the proposed approach extends naturally to the broad domain of learning via relaxed optimization techniques. Our results enable an assessment of the model vulnerability without requiring additional test data and operate in a distribution-free setup. These results not only provide a tool to enhance trust in the model's applicability but also aid in selecting among competing alternatives. Later in the paper, we show that our findings also offer useful insights for establishing new results within the out-of-distribution framework.

Signed-Perturbed Sums Estimation of ARX Systems: Exact Coverage and Strong Consistency (Extended Version)

Sign-Perturbed Sums (SPS) is a system identification method that constructs confidence regions for the unknown system parameters. In this paper, we study SPS for ARX systems, and establish that the confidence regions are guaranteed to include the true model parameter with exact, user-chosen, probability under mild statistical assumptions, a property that holds true for any finite number of observed input-output data. Furthermore, we prove the strong consistency of the method, that is, as the number of data points increases, the confidence region gets smaller and smaller and will asymptotically almost surely exclude any parameter value different from the true one. In addition, we also show that, asymptotically, the SPS region is included in an ellipsoid which is marginally larger than the confidence ellipsoid obtained from the asymptotic theory of system identification. The results are theoretically proven and illustrated in a simulation example.

Estimation of Accurate and Calibrated Uncertainties in Deterministic models

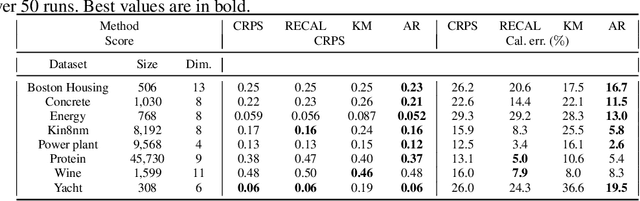
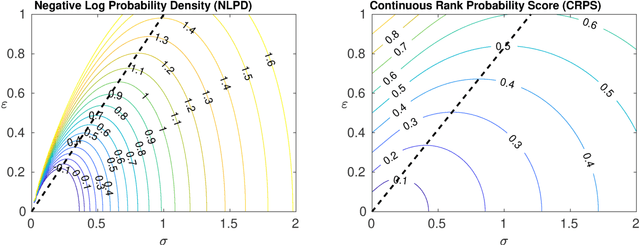
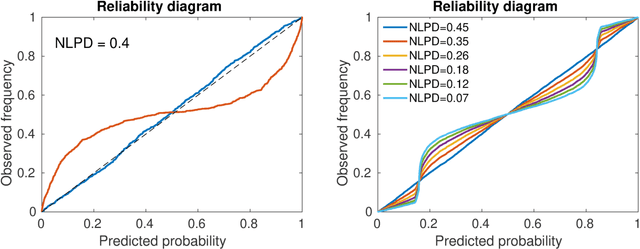
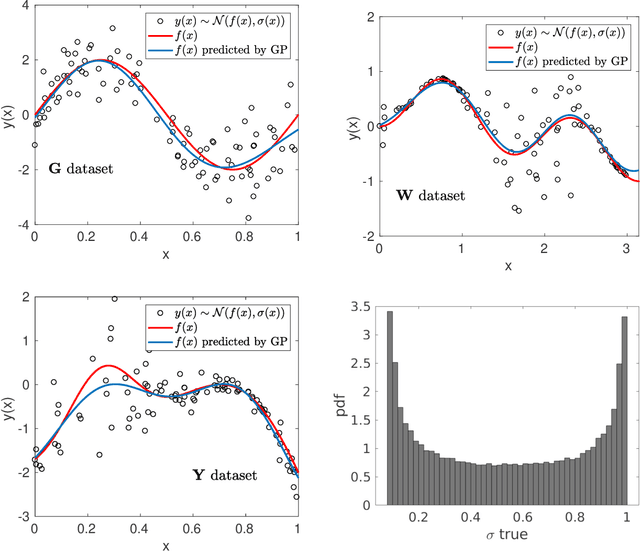
In this paper we focus on the problem of assigning uncertainties to single-point predictions generated by a deterministic model that outputs a continuous variable. This problem applies to any state-of-the-art physics or engineering models that have a computational cost that does not readily allow to run ensembles and to estimate the uncertainty associated to single-point predictions. Essentially, we devise a method to easily transform a deterministic prediction into a probabilistic one. We show that for doing so, one has to compromise between the accuracy and the reliability (calibration) of such a probabilistic model. Hence, we introduce a cost function that encodes their trade-off. We use the Continuous Rank Probability Score to measure accuracy and we derive an analytic formula for the reliability, in the case of forecasts of continuous scalar variables expressed in terms of Gaussian distributions. The new Accuracy-Reliability cost function is then used to estimate the input-dependent variance, given a black-box mean function, by solving a two-objective optimization problem. The simple philosophy behind this strategy is that predictions based on the estimated variances should not only be accurate, but also reliable (i.e. statistical consistent with observations). Conversely, early works based on the minimization of classical cost functions, such as the negative log probability density, cannot simultaneously enforce both accuracy and reliability. We show several examples both with synthetic data, where the underlying hidden noise can accurately be recovered, and with large real-world datasets.