Signed-Perturbed Sums Estimation of ARX Systems: Exact Coverage and Strong Consistency (Extended Version)

Sign-Perturbed Sums (SPS) is a system identification method that constructs confidence regions for the unknown system parameters. In this paper, we study SPS for ARX systems, and establish that the confidence regions are guaranteed to include the true model parameter with exact, user-chosen, probability under mild statistical assumptions, a property that holds true for any finite number of observed input-output data. Furthermore, we prove the strong consistency of the method, that is, as the number of data points increases, the confidence region gets smaller and smaller and will asymptotically almost surely exclude any parameter value different from the true one. In addition, we also show that, asymptotically, the SPS region is included in an ellipsoid which is marginally larger than the confidence ellipsoid obtained from the asymptotic theory of system identification. The results are theoretically proven and illustrated in a simulation example.

Compression, Generalization and Learning

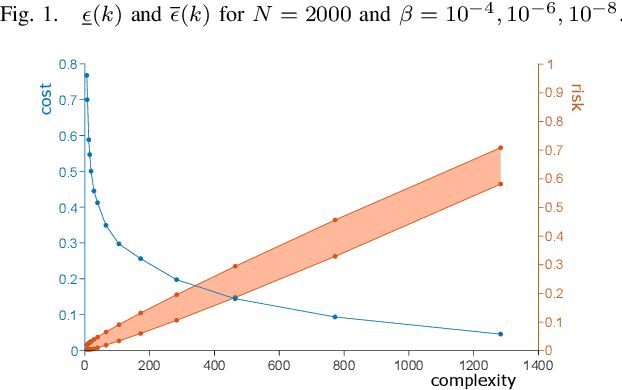
A compression function is a map that slims down an observational set into a subset of reduced size, while preserving its informational content. In multiple applications, the condition that one new observation makes the compressed set change is interpreted that this observation brings in extra information and, in learning theory, this corresponds to misclassification, or misprediction. In this paper, we lay the foundations of a new theory that allows one to keep control on the probability of change of compression (called the "risk"). We identify conditions under which the cardinality of the compressed set is a consistent estimator for the risk (without any upper limit on the size of the compressed set) and prove unprecedentedly tight bounds to evaluate the risk under a generally applicable condition of preference. All results are usable in a fully agnostic setup, without requiring any a priori knowledge on the probability distribution of the observations. Not only these results offer a valid support to develop trust in observation-driven methodologies, they also play a fundamental role in learning techniques as a tool for hyper-parameter tuning.

Scenario optimization with relaxation: a new tool for design and application to machine learning problems

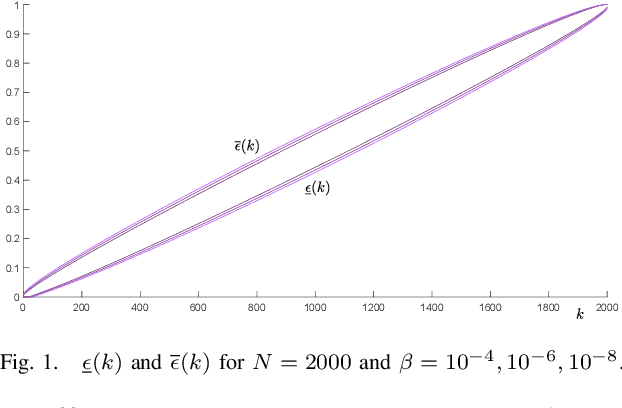
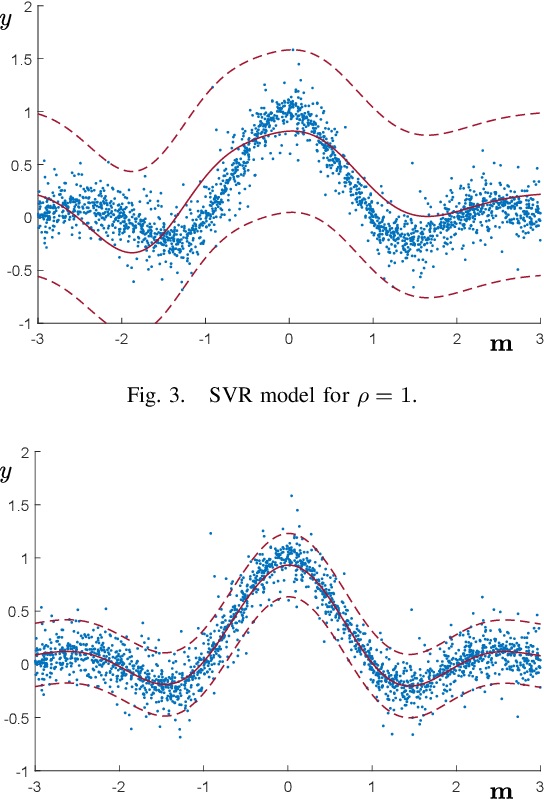
Scenario optimization is by now a well established technique to perform designs in the presence of uncertainty. It relies on domain knowledge integrated with first-hand information that comes from data and generates solutions that are also accompanied by precise statements of reliability. In this paper, following recent developments in (Garatti and Campi, 2019), we venture beyond the traditional set-up of scenario optimization by analyzing the concept of constraints relaxation. By a solid theoretical underpinning, this new paradigm furnishes fundamental tools to perform designs that meet a proper compromise between robustness and performance. After suitably expanding the scope of constraints relaxation as proposed in (Garatti and Campi, 2019), we focus on various classical Support Vector methods in machine learning - including SVM (Support Vector Machine), SVR (Support Vector Regression) and SVDD (Support Vector Data Description) - and derive new results for the ability of these methods to generalize.

Sign-Perturbed Sums: A New System Identification Approach for Constructing Exact Non-Asymptotic Confidence Regions in Linear Regression Models

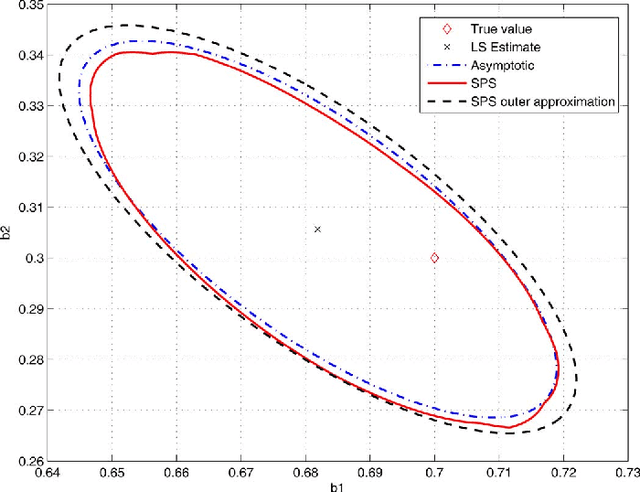
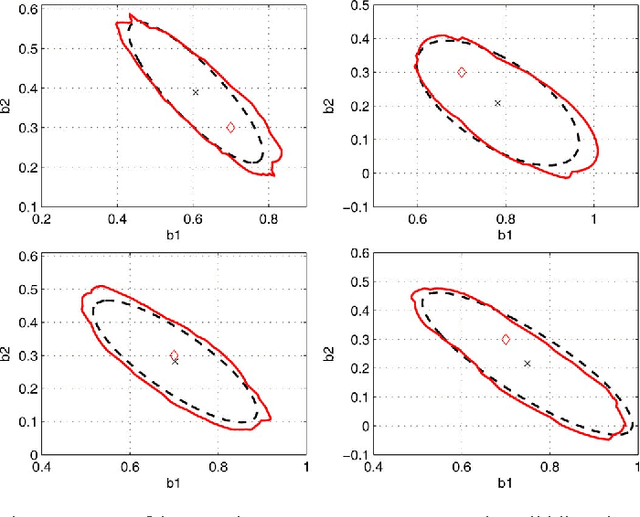
We propose a new system identification method, called Sign-Perturbed Sums (SPS), for constructing non-asymptotic confidence regions under mild statistical assumptions. SPS is introduced for linear regression models, including but not limited to FIR systems, and we show that the SPS confidence regions have exact confidence probabilities, i.e., they contain the true parameter with a user-chosen exact probability for any finite data set. Moreover, we also prove that the SPS regions are star convex with the Least-Squares (LS) estimate as a star center. The main assumptions of SPS are that the noise terms are independent and symmetrically distributed about zero, but they can be nonstationary, and their distributions need not be known. The paper also proposes a computationally efficient ellipsoidal outer approximation algorithm for SPS. Finally, SPS is demonstrated through a number of simulation experiments.