Simone Garatti
Risk Analysis and Design Against Adversarial Actions
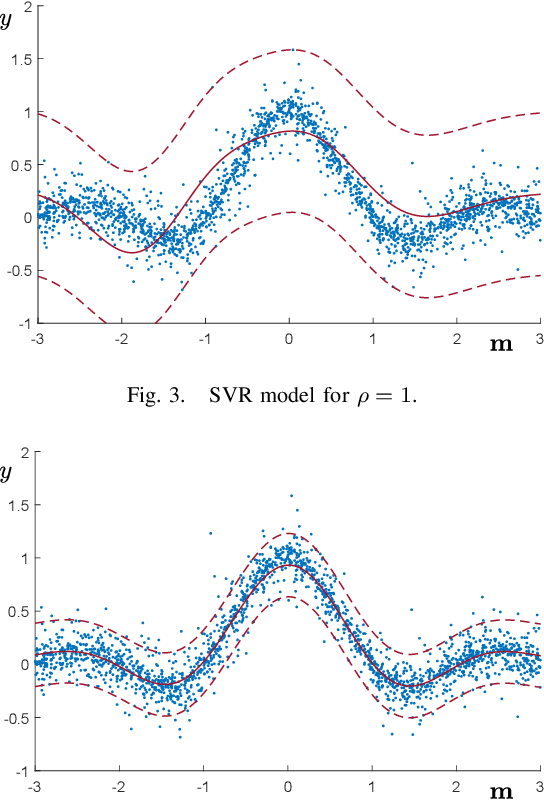
May 02, 2025Abstract:Learning models capable of providing reliable predictions in the face of adversarial actions has become a central focus of the machine learning community in recent years. This challenge arises from observing that data encountered at deployment time often deviate from the conditions under which the model was trained. In this paper, we address deployment-time adversarial actions and propose a versatile, well-principled framework to evaluate the model's robustness against attacks of diverse types and intensities. While we initially focus on Support Vector Regression (SVR), the proposed approach extends naturally to the broad domain of learning via relaxed optimization techniques. Our results enable an assessment of the model vulnerability without requiring additional test data and operate in a distribution-free setup. These results not only provide a tool to enhance trust in the model's applicability but also aid in selecting among competing alternatives. Later in the paper, we show that our findings also offer useful insights for establishing new results within the out-of-distribution framework.
Compression, Generalization and Learning
Jan 30, 2023



Abstract:A compression function is a map that slims down an observational set into a subset of reduced size, while preserving its informational content. In multiple applications, the condition that one new observation makes the compressed set change is interpreted that this observation brings in extra information and, in learning theory, this corresponds to misclassification, or misprediction. In this paper, we lay the foundations of a new theory that allows one to keep control on the probability of change of compression (called the "risk"). We identify conditions under which the cardinality of the compressed set is a consistent estimator for the risk (without any upper limit on the size of the compressed set) and prove unprecedentedly tight bounds to evaluate the risk under a generally applicable condition of preference. All results are usable in a fully agnostic setup, without requiring any a priori knowledge on the probability distribution of the observations. Not only these results offer a valid support to develop trust in observation-driven methodologies, they also play a fundamental role in learning techniques as a tool for hyper-parameter tuning.
Scenario optimization with relaxation: a new tool for design and application to machine learning problems
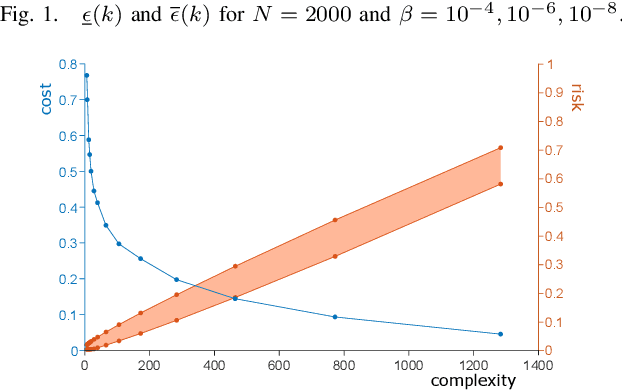
Apr 13, 2020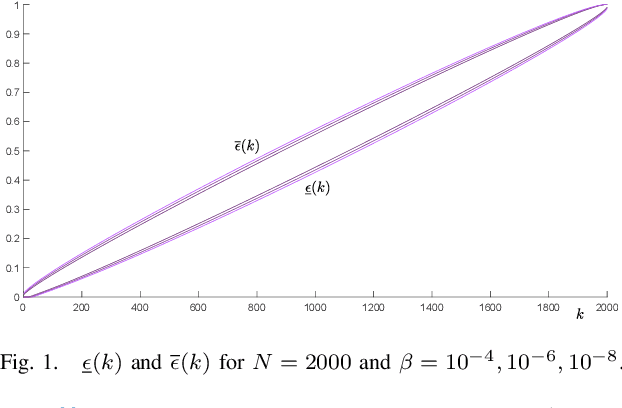

Abstract:Scenario optimization is by now a well established technique to perform designs in the presence of uncertainty. It relies on domain knowledge integrated with first-hand information that comes from data and generates solutions that are also accompanied by precise statements of reliability. In this paper, following recent developments in (Garatti and Campi, 2019), we venture beyond the traditional set-up of scenario optimization by analyzing the concept of constraints relaxation. By a solid theoretical underpinning, this new paradigm furnishes fundamental tools to perform designs that meet a proper compromise between robustness and performance. After suitably expanding the scope of constraints relaxation as proposed in (Garatti and Campi, 2019), we focus on various classical Support Vector methods in machine learning - including SVM (Support Vector Machine), SVR (Support Vector Regression) and SVDD (Support Vector Data Description) - and derive new results for the ability of these methods to generalize.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge