Alexandru Nicolau
Molecular Classification Using Hyperdimensional Graph Classification
Mar 18, 2024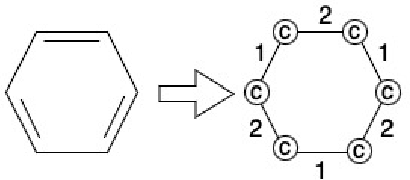
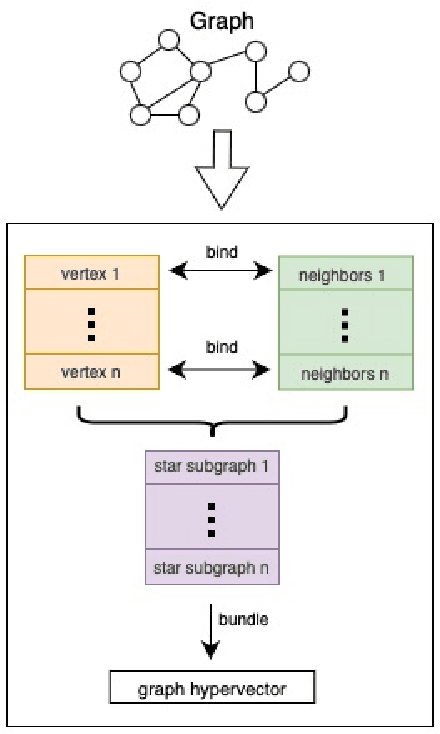
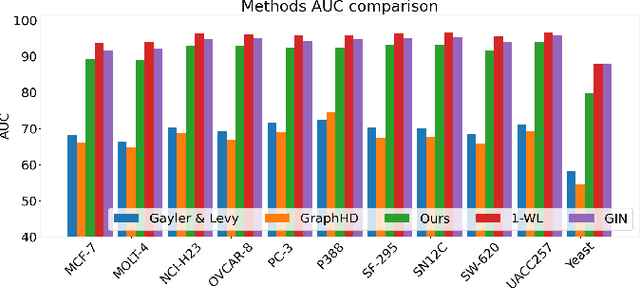
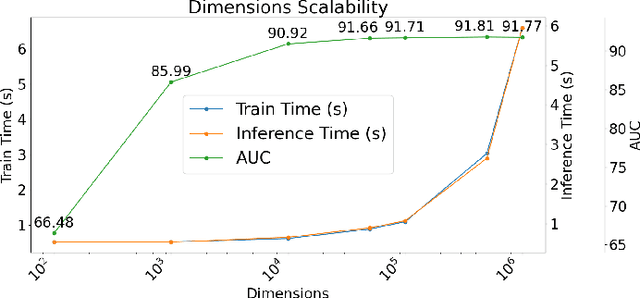
Abstract:Our work introduces an innovative approach to graph learning by leveraging Hyperdimensional Computing. Graphs serve as a widely embraced method for conveying information, and their utilization in learning has gained significant attention. This is notable in the field of chemoinformatics, where learning from graph representations plays a pivotal role. An important application within this domain involves the identification of cancerous cells across diverse molecular structures. We propose an HDC-based model that demonstrates comparable Area Under the Curve results when compared to state-of-the-art models like Graph Neural Networks (GNNs) or the Weisfieler-Lehman graph kernel (WL). Moreover, it outperforms previously proposed hyperdimensional computing graph learning methods. Furthermore, it achieves noteworthy speed enhancements, boasting a 40x acceleration in the training phase and a 15x improvement in inference time compared to GNN and WL models. This not only underscores the efficacy of the HDC-based method, but also highlights its potential for expedited and resource-efficient graph learning.
Enhanced Detection of Transdermal Alcohol Levels Using Hyperdimensional Computing on Embedded Devices
Mar 18, 2024Abstract:Alcohol consumption has a significant impact on individuals' health, with even more pronounced consequences when consumption becomes excessive. One approach to promoting healthier drinking habits is implementing just-in-time interventions, where timely notifications indicating intoxication are sent during heavy drinking episodes. However, the complexity or invasiveness of an intervention mechanism may deter an individual from using them in practice. Previous research tackled this challenge using collected motion data and conventional Machine Learning (ML) algorithms to classify heavy drinking episodes, but with impractical accuracy and computational efficiency for mobile devices. Consequently, we have elected to use Hyperdimensional Computing (HDC) to design a just-in-time intervention approach that is practical for smartphones, smart wearables, and IoT deployment. HDC is a framework that has proven results in processing real-time sensor data efficiently. This approach offers several advantages, including low latency, minimal power consumption, and high parallelism. We explore various HDC encoding designs and combine them with various HDC learning models to create an optimal and feasible approach for mobile devices. Our findings indicate an accuracy rate of 89\%, which represents a substantial 12\% improvement over the current state-of-the-art.
Always-Sparse Training by Growing Connections with Guided Stochastic Exploration
Jan 12, 2024Abstract:The excessive computational requirements of modern artificial neural networks (ANNs) are posing limitations on the machines that can run them. Sparsification of ANNs is often motivated by time, memory and energy savings only during model inference, yielding no benefits during training. A growing body of work is now focusing on providing the benefits of model sparsification also during training. While these methods greatly improve the training efficiency, the training algorithms yielding the most accurate models still materialize the dense weights, or compute dense gradients during training. We propose an efficient, always-sparse training algorithm with excellent scaling to larger and sparser models, supported by its linear time complexity with respect to the model width during training and inference. Moreover, our guided stochastic exploration algorithm improves over the accuracy of previous sparse training methods. We evaluate our method on CIFAR-10/100 and ImageNet using ResNet, VGG, and ViT models, and compare it against a range of sparsification methods.
DotHash: Estimating Set Similarity Metrics for Link Prediction and Document Deduplication
May 27, 2023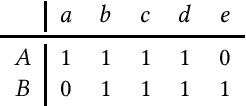
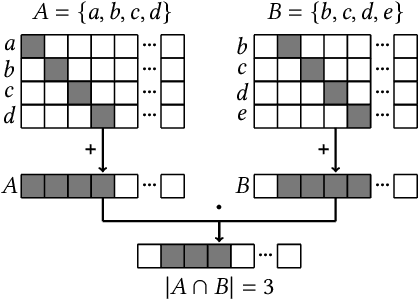
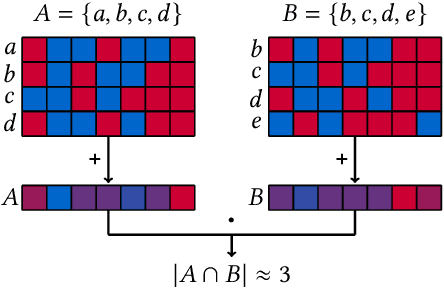
Abstract:Metrics for set similarity are a core aspect of several data mining tasks. To remove duplicate results in a Web search, for example, a common approach looks at the Jaccard index between all pairs of pages. In social network analysis, a much-celebrated metric is the Adamic-Adar index, widely used to compare node neighborhood sets in the important problem of predicting links. However, with the increasing amount of data to be processed, calculating the exact similarity between all pairs can be intractable. The challenge of working at this scale has motivated research into efficient estimators for set similarity metrics. The two most popular estimators, MinHash and SimHash, are indeed used in applications such as document deduplication and recommender systems where large volumes of data need to be processed. Given the importance of these tasks, the demand for advancing estimators is evident. We propose DotHash, an unbiased estimator for the intersection size of two sets. DotHash can be used to estimate the Jaccard index and, to the best of our knowledge, is the first method that can also estimate the Adamic-Adar index and a family of related metrics. We formally define this family of metrics, provide theoretical bounds on the probability of estimate errors, and analyze its empirical performance. Our experimental results indicate that DotHash is more accurate than the other estimators in link prediction and detecting duplicate documents with the same complexity and similar comparison time.
HDCC: A Hyperdimensional Computing compiler for classification on embedded systems and high-performance computing
Apr 24, 2023
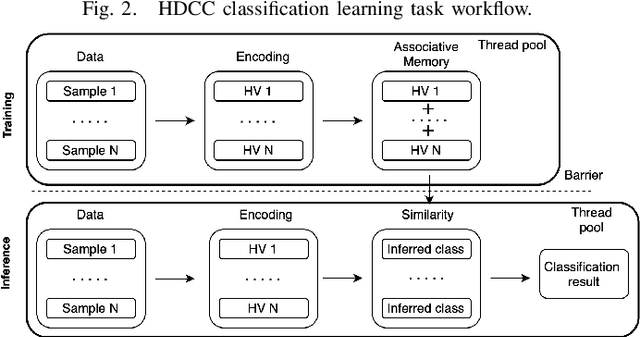
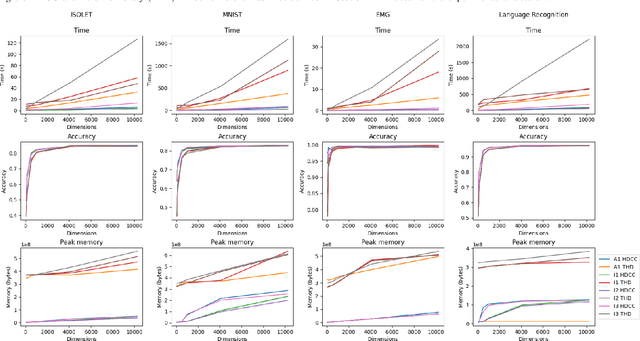
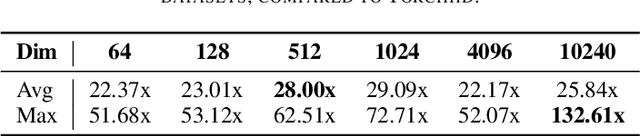
Abstract:Hyperdimensional Computing (HDC) is a bio-inspired computing framework that has gained increasing attention, especially as a more efficient approach to machine learning (ML). This work introduces the \name{} compiler, the first open-source compiler that translates high-level descriptions of HDC classification methods into optimized C code. The code generated by the proposed compiler has three main features for embedded systems and High-Performance Computing: (1) it is self-contained and has no library or platform dependencies; (2) it supports multithreading and single instruction multiple data (SIMD) instructions using C intrinsics; (3) it is optimized for maximum performance and minimal memory usage. \name{} is designed like a modern compiler, featuring an intuitive and descriptive input language, an intermediate representation (IR), and a retargetable backend. This makes \name{} a valuable tool for research and applications exploring HDC for classification tasks on embedded systems and High-Performance Computing. To substantiate these claims, we conducted experiments with HDCC on several of the most popular datasets in the HDC literature. The experiments were run on four different machines, including different hyperparameter configurations, and the results were compared to a popular prototyping library built on PyTorch. The results show a training and inference speedup of up to 132x, averaging 25x across all datasets and machines. Regarding memory usage, using 10240-dimensional hypervectors, the average reduction was 5x, reaching up to 14x. When considering vectors of 64 dimensions, the average reduction was 85x, with a maximum of 158x less memory utilization.
Torchhd: An Open-Source Python Library to Support Hyperdimensional Computing Research
May 18, 2022
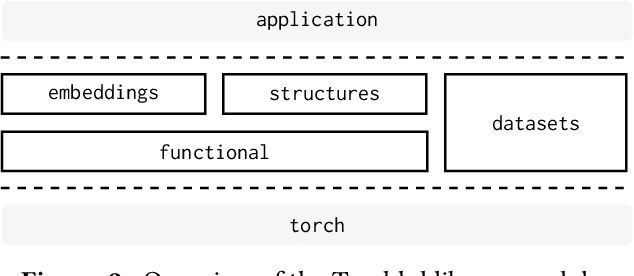
Abstract:Hyperdimensional Computing (HDC) is a neuro-inspired computing framework that exploits high-dimensional random vector spaces. HDC uses extremely parallelizable arithmetic to provide computational solutions that balance accuracy, efficiency and robustness. This has proven especially useful in resource-limited scenarios such as embedded systems. The commitment of the scientific community to aggregate and disseminate research in this particularly multidisciplinary field has been fundamental for its advancement. Adding to this effort, we propose Torchhd, a high-performance open-source Python library for HDC. Torchhd seeks to make HDC more accessible and serves as an efficient foundation for research and application development. The easy-to-use library builds on top of PyTorch and features state-of-the-art HDC functionality, clear documentation and implementation examples from notable publications. Comparing publicly available code with their Torchhd implementation shows that experiments can run up to 104$\times$ faster. Torchhd is available at: https://github.com/hyperdimensional-computing/torchhd
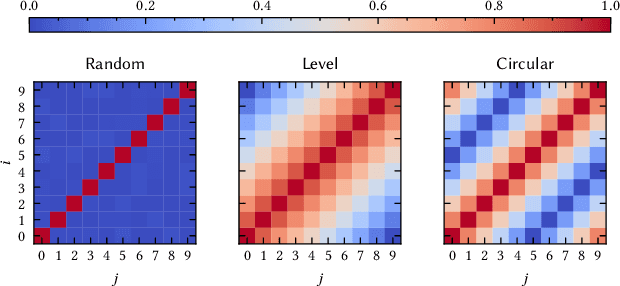
An Extension to Basis-Hypervectors for Learning from Circular Data in Hyperdimensional Computing
May 16, 2022
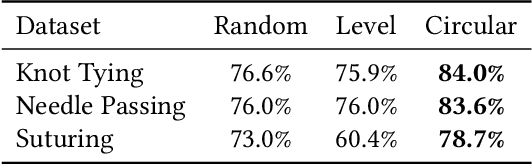
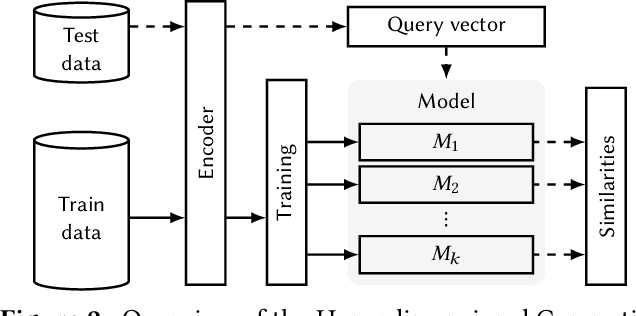

Abstract:Hyperdimensional Computing (HDC) is a computation framework based on properties of high-dimensional random spaces. It is particularly useful for machine learning in resource-constrained environments, such as embedded systems and IoT, as it achieves a good balance between accuracy, efficiency and robustness. The mapping of information to the hyperspace, named encoding, is the most important stage in HDC. At its heart are basis-hypervectors, responsible for representing the smallest units of meaningful information. In this work we present a detailed study on basis-hypervector sets, which leads to practical contributions to HDC in general: 1) we propose an improvement for level-hypervectors, used to encode real numbers; 2) we introduce a method to learn from circular data, an important type of information never before addressed in machine learning with HDC. Empirical results indicate that these contributions lead to considerably more accurate models for both classification and regression with circular data.
GraphHD: Efficient graph classification using hyperdimensional computing
May 16, 2022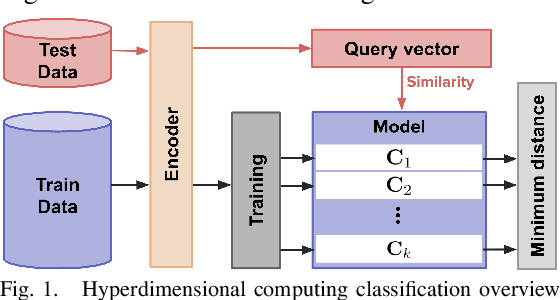
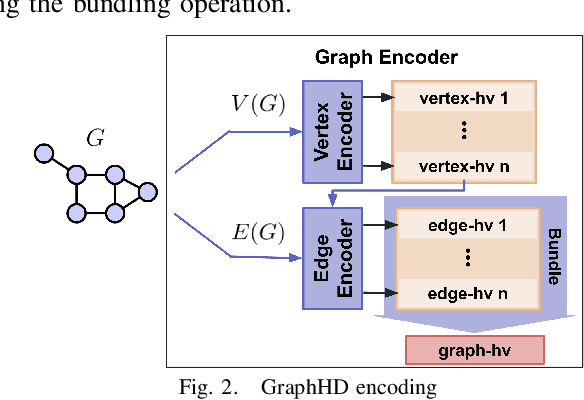
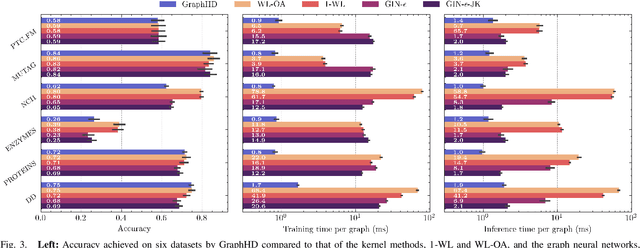
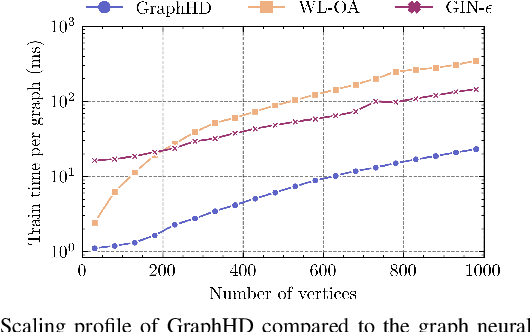
Abstract:Hyperdimensional Computing (HDC) developed by Kanerva is a computational model for machine learning inspired by neuroscience. HDC exploits characteristics of biological neural systems such as high-dimensionality, randomness and a holographic representation of information to achieve a good balance between accuracy, efficiency and robustness. HDC models have already been proven to be useful in different learning applications, especially in resource-limited settings such as the increasingly popular Internet of Things (IoT). One class of learning tasks that is missing from the current body of work on HDC is graph classification. Graphs are among the most important forms of information representation, yet, to this day, HDC algorithms have not been applied to the graph learning problem in a general sense. Moreover, graph learning in IoT and sensor networks, with limited compute capabilities, introduce challenges to the overall design methodology. In this paper, we present GraphHD$-$a baseline approach for graph classification with HDC. We evaluate GraphHD on real-world graph classification problems. Our results show that when compared to the state-of-the-art Graph Neural Networks (GNNs) the proposed model achieves comparable accuracy, while training and inference times are on average 14.6$\times$ and 2.0$\times$ faster, respectively.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge